题目内容
3.质量为m、带电量为+q的小球处于方向竖直向上、范围足够大的匀强电场中,由空中A点无初速度释放,在t秒末撤去匀强电场,再经过t秒小球又回到A点.不计空气阻力则( )| A. | 电场强度的大小为$E=\frac{4mg}{3q}$ | |
| B. | 整个过程中电场力对小球做功为$\frac{2}{9}m{g^2}{t^2}$ | |
| C. | 小球回到A点时的速度大小为$\frac{2}{3}gt$ | |
| D. | 从A点到最高点小球重力势能变化了$\frac{1}{6}m{g^2}{t^2}$ |
分析 分析小球的运动情况:小球先向上做匀加速运动,撤去匀强电场后小球向上做匀减速运动,最后向下匀加速运动,即做自由落体运动.由运动学公式求出t秒末速度大小,撤去电场后小球运动,看成竖直上抛运动的位移与这个匀加速运动的位移大小相等、方向相反,根据牛顿第二定律和运动学公式结合求电场强度;对全过程运用动能定理求出电场力做功的大小;由动能定理得求出A点到最高点的高度,得到重力势能的减小量.
解答 解:AC、小球先做匀加速运动,后做竖直上抛运动,两个过程的位移大小相等、方向相反.
设电场强度大小为E,有电场时小球的加速度大小为a,取竖直向上方向为正方向,则:$\frac{1}{2}$at2=-(vt-$\frac{1}{2}$gt2)
又因有:v=at
解得:a=$\frac{1}{3}$g,
则小球回到A点时的速度为:v′=v-gt=-$\frac{2}{3}gt$
由牛顿第二定律得:
a=$\frac{qE-mg}{m}$,
解得:qE=$\frac{4}{3}$mg.
则电场强度为:E=$\frac{4}{3}mg$.故A、C正确.
B、取向上匀加速运动过程,运用动能定理得,设电场力做功为W,则有:W-mg×$\frac{1}{2}×\frac{1}{3}g{t}^{2}$=$\frac{1}{2}$m($\frac{1}{3}$gt)2,解得:W=$\frac{2}{9}m{g^2}{t^2}$.故B正确.
D、设从A点到最高点的高度为h,根据动能定理得:
mgh-qE(h-$\frac{1}{2}$×$\frac{1}{3}$gt2)=0,
解得:h=$\frac{2}{9}$gt2.
从A点到最高点小球重力势能增加了:△Ep=mgh=$\frac{2}{9}m{g^2}{t^2}$.故D错误.
故选:ABC.
点评 本题首先要分析小球的运动过程,采用整体法研究竖直上抛运动过程,抓住两个过程之间的联系:位移大小相等、方向相反,运用牛顿第二定律、运动学规律和动能定理结合进行研究.

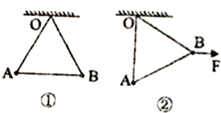 如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )
如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | ||
| C. | $\sqrt{3}$ | D. | 条件不足,无法确定 |
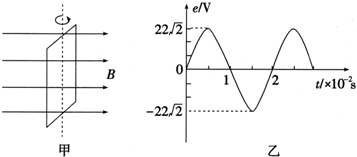
| A. | t=0.01s时穿过线框的磁通量最小 | |
| B. | 该交流电电动势的有效值为$11\sqrt{2}V$ | |
| C. | 该交流电电动势的瞬时值表达式为e=22$\sqrt{2}sin({100π})tV$ | |
| D. | 在1s内电流方向改变100次 |
| A. | $\frac{1}{\frac{1}{{T}_{0}}-\frac{1}{2π}\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{1}{\frac{1}{{T}_{0}}+\frac{1}{2π}\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | 2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$ | D. | T0-2π$\sqrt{\frac{g{R}^{3}}{{r}^{3}}}$ |
 如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )
如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )| A. | 该同学做了两次下蹲-起立的动作 | |
| B. | 该同学做了四次下蹲-起立的动作 | |
| C. | 下蹲过程中人处于失重状态 | |
| D. | 下蹲过程中人处于超重状态,后处于失重状态 |
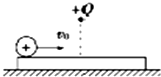 如图所示,在水平放置的粗糙金属板中心正上方有一带正电的点电荷Q,另一表面绝缘、带正电的金属小球(可视为质点,且不影响原电场)自左以初速度v0 在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的粗糙金属板中心正上方有一带正电的点电荷Q,另一表面绝缘、带正电的金属小球(可视为质点,且不影响原电场)自左以初速度v0 在金属板上向右运动,在运动过程中( )| A. | 小球可能做加速度增大的减速运动 | |
| B. | 小球做匀速直线运动 | |
| C. | 小球受到的静电力对小球先做负功,后做正功 | |
| D. | 小球受到的静电力对小球先做正功,后做负功 |
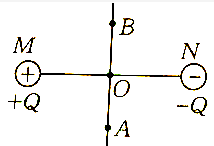 如图所示,真空中电荷量分别为+Q和-Q的点电荷M、N相距r,AOB在其中垂线上,当电子沿等量异种电荷的中垂线由A→O→B移动,则电子所受的电场力的大小和方向变化情况是( )
如图所示,真空中电荷量分别为+Q和-Q的点电荷M、N相距r,AOB在其中垂线上,当电子沿等量异种电荷的中垂线由A→O→B移动,则电子所受的电场力的大小和方向变化情况是( )| A. | 先变大后变小,方向水平向左 | B. | 先变大后变小,方向水平向右 | ||
| C. | 先变小后变大,方向水平向左 | D. | 先变小后变大,方向水平向右 |
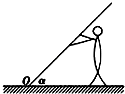 如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )
如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )| A. | ω=$\frac{{v{{cos}^2}α}}{h}$ | B. | ω=$\frac{vsinα}{h}$ | C. | ω=$\frac{{v{{sin}^2}α}}{h}$ | D. | ω=$\frac{v}{hsinα}$ |
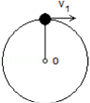 如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求
如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求