题目内容
15.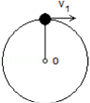 如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求
如图所示,质量m=0.1kg的小球在细绳的拉力作用下载竖直面内做半径为r=0.2m的圆周运动,g取10m/s2,求(1)小球通过最高点时的速度至少为多少?
(2)若小球在最高点的速率为v1=2m/s,则小球在最高点时的细绳的拉力是多少?
分析 (1)小球恰好通过最高点时,细绳的拉力为零,由重力提供向心力,可由牛顿第二定律求出小球通过最高点时的速度;
(2)在最高点,根据牛顿第二定律列式即可求解.
解答 解:(1)当小球恰好通过最高点时,细绳的拉力为零,由重力提供向心力,可由牛顿第二定律得:
mg=$m\frac{{{v}_{0}}^{2}}{r}$
解得:v0=$\sqrt{gr}=\sqrt{0.2×10}=\sqrt{2}m/s$
(2)在最高点,根据牛顿第二定律得:
mg+T=$m\frac{{{v}_{1}}^{2}}{r}$
解得:T=$0.1×\frac{4}{0.2}-0.1×10$=1N
答:(1)小球通过最高点时的速度至少为$\sqrt{2}$;
(2)若小球在最高点的速率为v1=2m/s,则小球在最高点时的细绳的拉力为1N.
点评 本题中小球到达最高点的临界速度为v0=$\sqrt{gr}$,关键通过分析受力,确定向心力的来源,难度不大,属于基础题.

练习册系列答案
相关题目
2. 一个质量m=0.05kg的小球做平抛运动时,测出小球在不同时刻速率v的数据,并作出v2-t2图线,如图所示.不计空气阻力,下列说法正确的是( )
一个质量m=0.05kg的小球做平抛运动时,测出小球在不同时刻速率v的数据,并作出v2-t2图线,如图所示.不计空气阻力,下列说法正确的是( )
 一个质量m=0.05kg的小球做平抛运动时,测出小球在不同时刻速率v的数据,并作出v2-t2图线,如图所示.不计空气阻力,下列说法正确的是( )
一个质量m=0.05kg的小球做平抛运动时,测出小球在不同时刻速率v的数据,并作出v2-t2图线,如图所示.不计空气阻力,下列说法正确的是( )| A. | 小球的初速度为2m/s | |
| B. | 图线的斜率大小为100m2•s-4 | |
| C. | 横轴读数在0.16时,小球离抛出点的位移大小为2m | |
| D. | 横轴读数在0~0.25区间内,小球所受重力做功的平均功率为1.25W |
3.质量为m、带电量为+q的小球处于方向竖直向上、范围足够大的匀强电场中,由空中A点无初速度释放,在t秒末撤去匀强电场,再经过t秒小球又回到A点.不计空气阻力则( )
| A. | 电场强度的大小为$E=\frac{4mg}{3q}$ | |
| B. | 整个过程中电场力对小球做功为$\frac{2}{9}m{g^2}{t^2}$ | |
| C. | 小球回到A点时的速度大小为$\frac{2}{3}gt$ | |
| D. | 从A点到最高点小球重力势能变化了$\frac{1}{6}m{g^2}{t^2}$ |
3.用电流表和电压表测定电池的电动势E和内阻r,所用电路如图1所示.

(1)根据本实验需要,选定器材和量程,按照电路图连接上方的实物图(图2).
(2)k连接电路后,一位同学将测得的六组数据如下表所示.
试根据这些数据在图3中作出U-I图线.
(3)根据图线求出电池的电动势E=1.50V,电池的内阻r=0.83Ω

(1)根据本实验需要,选定器材和量程,按照电路图连接上方的实物图(图2).
(2)k连接电路后,一位同学将测得的六组数据如下表所示.
试根据这些数据在图3中作出U-I图线.
(3)根据图线求出电池的电动势E=1.50V,电池的内阻r=0.83Ω
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电流I/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
| 电压U/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.10 | 1.05 |
10.如图所示的电路中,P、Q为两个相同的灯泡,自感线圈L的电阻不计,则下列说法正确的是( )

| A. | S接通瞬间,P、Q同时达到正常发光 | |
| B. | S断开瞬间,P立即熄灭,Q突然闪亮然后熄灭 | |
| C. | S断开瞬间,通过P的电流从右向左 | |
| D. | S断开瞬间,通过Q的电流与原来方向相反 |
20. 在如图所示的电路中,a、b为两个完全相同的灯泡,L为自感线圈(电阻为0),E为电源,S为开关.关于两灯泡点亮和熄灭的先后次序,下列说法中正确的是( )
在如图所示的电路中,a、b为两个完全相同的灯泡,L为自感线圈(电阻为0),E为电源,S为开关.关于两灯泡点亮和熄灭的先后次序,下列说法中正确的是( )
 在如图所示的电路中,a、b为两个完全相同的灯泡,L为自感线圈(电阻为0),E为电源,S为开关.关于两灯泡点亮和熄灭的先后次序,下列说法中正确的是( )
在如图所示的电路中,a、b为两个完全相同的灯泡,L为自感线圈(电阻为0),E为电源,S为开关.关于两灯泡点亮和熄灭的先后次序,下列说法中正确的是( )| A. | 合上开关,a,b立即正常发光 | |
| B. | 合上开关,b立即发光;a逐渐变亮,直至正常发光 | |
| C. | 断开开关,a,b立即熄灭 | |
| D. | 断开开关,b立即熄灭、a逐渐熄灭 |
7.关于平抛运动,下列说法错误的是( )
| A. | 平抛运动是匀变速运动 | |
| B. | 平抛运动是加速曲线运动 | |
| C. | 做平抛运动的物体处于完全失重状态 | |
| D. | 做平抛运动的物体,落地时间和落地时的速度只与抛出点的高度有关 |
4.一个物体做自由落体运动,重力加速度g取1Om/s2.该物体( )
| A. | 第2s末的速度大小为1Om/s | B. | 第2s末的速度大小为30m/s | ||
| C. | 在前3s内下落的距离为45m | D. | 在前3s内下落的距离为60m |
5. 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度一直保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度一直保持不变,则( )
 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度一直保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度一直保持不变,则( )| A. | F的功率减小 | B. | F的功率不变 | C. | F先增大后减小 | D. | F一直增大 |