题目内容
13. 如图所示,小车A通过一根绕过定滑轮的轻绳吊起一重物B,开始时用力按住A使A不动,现设法使A以速度vA=4m/s向左做匀速运动,某时刻连接A车右端的轻绳与水平方向成θ=370角,设此时B的速度大小为vB,(cos37°=0.8),不计空气阻力,忽略绳与滑轮间摩擦,则( )
如图所示,小车A通过一根绕过定滑轮的轻绳吊起一重物B,开始时用力按住A使A不动,现设法使A以速度vA=4m/s向左做匀速运动,某时刻连接A车右端的轻绳与水平方向成θ=370角,设此时B的速度大小为vB,(cos37°=0.8),不计空气阻力,忽略绳与滑轮间摩擦,则( )| A. | A不动时B对轻绳的拉力就是B的重力 | |
| B. | 当轻绳与水平方向成θ角时重物B的速度vB=5m/s | |
| C. | 当轻绳与水平方向成θ角时重物B的速度vB=3.2m/s | |
| D. | B上升到滑轮处前的过程中处于超重状态 |
分析 将汽车的运动分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于重物的速度大小,从而判断出重物的运动规律.
解答  解:A、若A不动时B对轻绳的拉力大小等于B的重力,不是同一个力,故A错误;
解:A、若A不动时B对轻绳的拉力大小等于B的重力,不是同一个力,故A错误;
BC、小车的运动可分解为沿绳方向和垂直于绳的方向的两个运动,因斜拉绳子与水平面的夹角为37°,由几何关系可得:vB=vAcos37°=3.2m/s;故B错误,C正确;
D、因汽车匀速直线运动,而θ逐渐变小,故vB逐渐变大,物体有向上的加速度,则B处于超重状态,故D正确.
故选:CD.
点评 解决本题的关键将汽车的运动分解为沿绳子方向和垂直于绳子方向,知道沿绳子方向的速度等于重物的速度大小.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
1. 如图所示的长方体是用电阻率为ρ的均匀金属制成的,长度为2L,其横截面为正方形,边长为L,若将它的a、b端接入电路时的电阻为R,则将它的两个侧面上的c、d端接入电路时的电阻是( )
如图所示的长方体是用电阻率为ρ的均匀金属制成的,长度为2L,其横截面为正方形,边长为L,若将它的a、b端接入电路时的电阻为R,则将它的两个侧面上的c、d端接入电路时的电阻是( )
 如图所示的长方体是用电阻率为ρ的均匀金属制成的,长度为2L,其横截面为正方形,边长为L,若将它的a、b端接入电路时的电阻为R,则将它的两个侧面上的c、d端接入电路时的电阻是( )
如图所示的长方体是用电阻率为ρ的均匀金属制成的,长度为2L,其横截面为正方形,边长为L,若将它的a、b端接入电路时的电阻为R,则将它的两个侧面上的c、d端接入电路时的电阻是( )| A. | R | B. | $\frac{R}{4}$ | C. | $\frac{R}{2}$ | D. | 4R |
2.以下关于物体做圆周运动时,正确的说法是( )
| A. | 所受到的合外力一定指向圆心 | |
| B. | 速度的大小可以不变,速度的方向一定改变 | |
| C. | 转得越快,加速度越大 | |
| D. | 线速度与圆周运动的半径成反比,角速度与圆周运动的半径成正比 |
1.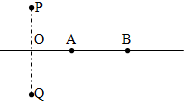 如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
 如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )| A. | EA一定大于EB,φA一定大于φB | B. | EA不一定大于EB,φA一定大于φB | ||
| C. | EA一定大于EB,φA不一定大于φB | D. | EA不一定大于EB,φA不一定大于φB |
8.图中甲、乙、丙是中学物理课本必修1中推导匀变速直线运动的位移公式所用的速度图象,下列说法正确的是( )


| A. | 推导中把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 | |
| B. | 甲图用矩形面积的和表示位移大小比丙图用梯形面积表示位移大小更接近真实值 | |
| C. | 这种用面积表示位移的方法只适用于匀变速直线运动 | |
| D. | 若丙图中纵坐标表示运动的加速度,则梯形面积表示加速度的变化量 |
18.用力传感器悬挂一钩码,一段时间后,钩码在拉力作用下沿竖直方向由静止开始运动.如图所示,图中实线是传感器记录的拉力大小变化情况,则( )
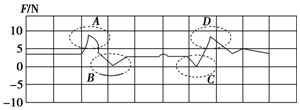

| A. | 钩码的重力约为4 N | |
| B. | 钩码的重力约为2 N | |
| C. | A、B、C、D四段图线中,钩码处于超重状态的是A、D,失重状态的是B、C | |
| D. | A、B、C、D四段图线中,钩码处于超重状态的是A、B,失重状态的是C、D |
5.一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,T>0.6s,a,b,c,P,Q是介质中的质点,则以下说法正确的是( )


| A. | 这列波的波速为50m/s | |
| B. | 质点a在这段时间内通过的路程等于30cm | |
| C. | 质点c在这段时间内通过的路程为20cm | |
| D. | t+0.5s时刻,质点b、P的位移相同 | |
| E. | c点开始振动的方向为-y方向 |
3.以下的计时数据指时间的是( )
| A. | 上海开往北京的620次列车于13时35分从上海发车 | |
| B. | 某人用13s跑完100m | |
| C. | 中央电视台新闻联播节目19时开播 | |
| D. | 某场足球赛开赛15min时甲队攻入一球 |