题目内容
2.在如图甲所示的半径为r的竖直圆柱形区域内,存在竖直向上的匀强磁场,磁感应强度大小随时间的变化关系为B=kt(k>0且为常量).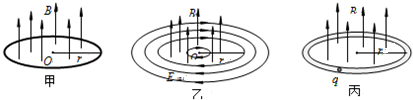
(1)将一由细导线构成的半径为r、电阻为R0的导体圆环水平固定在上述磁场中,并使圆环中心与磁场区域的中心重合.求在T时间内导体圆环产生的焦耳热.
(2)上述导体圆环之所以会产生电流是因为变化的磁场会在空间激发涡旋电场,该涡旋电场趋使导体内的自由电荷定向移动,形成电流.如图乙所示,变化的磁场产生的涡旋电场存在于磁场内外的广阔空间中,其电场线是在水平面内的一系列沿顺时针方向的同心圆(从上向下看),圆心与磁场区域的中心重合.在半径为r的圆周上,涡旋电场的电场强度大小处处相等,并且可以用E涡=$\frac{?}{2πr}$,其中ε为由于磁场变化在半径为r的导体圆环中产生的感生电动势.如图丙所示,在磁场区域的水平面内固定一个内壁光滑的绝缘环形真空细管道,其内环半径为r,管道中心与磁场区域的中心重合.由于细管道半径远远小于r,因此细管道内各处电场强度大小可视为相等的.某时刻,将管道内电荷量为q的带正电小球由静止释放(小球的直径略小于真空细管道的直径),小球受到切向的涡旋电场力的作用而运动,该力将改变小球速度的大小.该涡旋电场力与电场强度的关系和静电力与电场强度的关系相同.假设小球在运动过程中其电荷量保持不变,忽略小球受到的重力、小球运动时激发的磁场以及相对论效应.
①若小球由静止经过一段时间加速,获得动能Em,求小球在这段时间内在真空细管道内运动的圈数;
②若在真空细管道内部空间加有方向竖直向上的恒定匀强磁场,小球开始运动后经过时间t0,小球与环形真空细管道之间恰好没有作用力,求在真空细管道内部所加磁场的磁感应强度的大小.
分析 (1)根据法拉第电磁感应定律,结合闭合电路欧姆定律,及焦耳定律,即可求解;
(2)根据题意,求得斡旋电场,再确定电场力的大小,根据动能定理,从而求出运动的圈数;再由运动的合成与分解,结合运动学公式与牛顿第二定律,即可求解.
解答 解:(1)导体圆环内的磁通量发生变化,将产生感生电动势,
根据法拉第电磁感应定律,感生电动势为$E=\frac{△Φ}{△t}=\frac{△Bs}{△t}$=πr2k,
$I=\frac{E}{{R}_{0}}=\frac{π{r}^{2}k}{{R}_{0}}$,
在T时间内导体圆环产生的焦耳热为:
Q=I2R0T,
解得$Q=\frac{T{π}^{2}{k}^{2}{r}^{4}}{{R}_{0}}$
(2)①根据题意可知,磁场变化将在真空管道处产生涡旋电场,该电场的电场强度为:
${E}_{电}=\frac{E}{2πr}=\frac{kr}{2}$,
小球在该电场中受到的电场力的作用,电场力的大小为:
$F={E}_{电}q=\frac{kqr}{2}$,
电场力的方向与真空管道相切,即与速度方向始终相同,小球将会被加速,动能增大,
根据动能定理可得 Fs=Em,小球运动的圈数为 $N=\frac{s}{2πr}$,
解得:N=$\frac{{E}_{m}}{kqπ{r}^{2}}$;
②小球的切向加速度大小为:$a=\frac{F}{m}=\frac{kqr}{2m}$,
由于小球沿速度方向受到大小恒定的电场力,所以经过时间t0,
小球的速度大小v满足v=at0,
小球沿管道做圆周运动,因为小球与管道之间没有相互作用力,所以,小球受到洛伦兹力提供小球的向心力,
设所加的洛伦兹力提供小球的向心力,设所加磁场的磁感应强度为B0,
则有:$qv{B}_{0}=\frac{m{v}^{2}}{r}$,
解得:${B}_{0}=\frac{1}{2}k{t}_{0}$.
答:(1)在T时间内导体圆环产生的焦耳热$\frac{T{π}^{2}{k}^{2}{r}^{4}}{{R}_{0}}$;
(2)①若小球由静止经过一段时间加速,获得动能Em,求小球在这段时间内在真空细管道内运动的圈数$\frac{{E}_{m}}{kqπ{r}^{2}}$;
②若在真空细管道内部空间加有方向竖直向上的恒定匀强磁场,小球开始运动后经过时间t0,小球与环形真空细管道之间恰好没有作用力,求在真空细管道内部所加磁场的磁感应强度的大小为$\frac{1}{2}k{t}_{0}$.
点评 考查电磁学与力学综合运用的内容,掌握法拉第电磁感应定律、闭合电路欧姆定律与焦耳定律的应用,理解动能定理及牛顿运动定理,
注意电场强度与电动势的符号区别,此题难度较大.

 阅读快车系列答案
阅读快车系列答案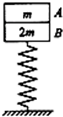 如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )| A. | 刚撤去外力F时,FN=$\frac{F+mg}{3}$ | B. | 弹簧弹力等于F时,FN=$\frac{F}{3}$ | ||
| C. | 当两物体速度最大时,FN=mg | D. | 当弹簧恢复原长时,FN=0 |

| A. | 3A | B. | 4A | C. | 5A | D. | 6A |
| A. | 这个反应既不是聚变反应也不是裂变反应 | |
| B. | 这个反应的核反应方程式$\left.\begin{array}{l}{2}\\{1}\end{array}\right.$H+$\left.\begin{array}{l}{3}\\{1}\end{array}\right.$H→$\left.\begin{array}{l}{4}\\{2}\end{array}\right.$He+$\left.\begin{array}{l}{1}\\{0}\end{array}\right.$n+γ | |
| C. | 辐射出的γ光子的能量E=(m3+m4-m1-m2)c2 | |
| D. | 辐射出的γ光子的波长λ=$\frac{h}{({m}_{1}+{m}_{2}-{m}_{3}-{m}_{4})c}$ |
| A. | 静止轨道卫星的向心加速度比中轨道卫星向心加速度大 | |
| B. | 静止轨道卫星和中轨道卫星的线速度均大于地球的第一宇宙速度 | |
| C. | 静止轨道卫星比中轨道卫星的周期大 | |
| D. | 地球赤道上随地球自转物体的向心加速度比静止轨道卫星向心加速度大 |
 如图所示,小物块位于半径为R=1m的光滑半球顶端,若将小物块无初速释放.求:
如图所示,小物块位于半径为R=1m的光滑半球顶端,若将小物块无初速释放.求: 在DIS中,光电门测量的是运动物体挡光时间内的平均速度,因为挡光片较窄,所以可看的是瞬时速度.为了测量做匀加速直线运动小车的加速度.将宽度均为b的挡光片A、B固定在小车上.如图所示.
在DIS中,光电门测量的是运动物体挡光时间内的平均速度,因为挡光片较窄,所以可看的是瞬时速度.为了测量做匀加速直线运动小车的加速度.将宽度均为b的挡光片A、B固定在小车上.如图所示. 如图所示,一个水平放罝的导热气缸,其中一端开口,一段封闭,导热的活塞在气缸内可以无摩擦的滑动,活塞与气缸之间密封完好.气缸底部与活塞之间密封有一定质量的理想气体,其温度为T,活塞的横截面积为S,活塞距离气缸底部为L,活塞自重产生的压强为O.5P0,此时活塞正处于静止状态.设大气压强为P0,外界环等温度不变.
如图所示,一个水平放罝的导热气缸,其中一端开口,一段封闭,导热的活塞在气缸内可以无摩擦的滑动,活塞与气缸之间密封完好.气缸底部与活塞之间密封有一定质量的理想气体,其温度为T,活塞的横截面积为S,活塞距离气缸底部为L,活塞自重产生的压强为O.5P0,此时活塞正处于静止状态.设大气压强为P0,外界环等温度不变.