题目内容
6.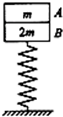 如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )| A. | 刚撤去外力F时,FN=$\frac{F+mg}{3}$ | B. | 弹簧弹力等于F时,FN=$\frac{F}{3}$ | ||
| C. | 当两物体速度最大时,FN=mg | D. | 当弹簧恢复原长时,FN=0 |
分析 刚撤去外力F时,先根据整体法求解出加速度,然后运用隔离法求解内力.当两物体速度最大时,合力为零.当弹簧恢复原长时,整体的加速度为g,再由牛顿第二定律求FN.
解答 解:A、在突然撤去F的瞬间,AB整体的合力向上,大小为F,根据牛顿第二定律,有:F=(m+2m)a,a=$\frac{F}{3m}$
对物体m受力分析,受重力和支持力,根据牛顿第二定律,有:FN-mg=ma;联立解得:FN=mg+$\frac{F}{3}$;故A错误.
B、弹簧弹力等于F时,根据牛顿第二定律得
对整体有:F-3mg=3ma
对m有:FN-mg=ma,联立解得 FN=$\frac{F}{3}$;故B正确.
C、当物体的合力为零时,速度最大,对m,由平衡条件得FN=mg.故C正确.
D、当弹簧恢复原长时,根据牛顿第二定律得
对整体有:3mg=3ma
对m有:mg-FN=ma,联立解得 FN=0;故D正确.
故选:BCD
点评 本题主要考查了牛顿第二定律的应用,关键要灵活选择研究对象,整体法和隔离法相结合运用,解答比较简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.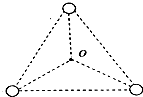 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )| A. | 每个星体受到向心力大小均为3$\frac{G{m}^{2}}{{a}^{2}}$ | |
| B. | 每个星体的角速度均为$\sqrt{\frac{3Gm}{{a}^{2}}}$ | |
| C. | 若a不变,m是原来的两倍,则周期是原来的$\frac{1}{2}$ | |
| D. | 若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$ |
11.国家体育总局会同国家环保部门从2010年初开始对将在广州进行的亚运会的所有场馆分期进行验收,其中有一项为放射性污染检测,因为建筑材料,如水泥、砖、混凝土中含有为了体现绿色奥运放射性元素氧.下列有关放射性的说法中正确的有( )
| A. | ${\;}_{90}^{238}U$衰变成20682pb要经过8次α衰变和6次β衰变 | |
| B. | 氧发生α衰变产生的α粒子是一种高速电子流,具有很强的穿透能力 | |
| C. | 放射性元素发生β衰变时所释放的电子是原子核内的中子转化为质子时产生的 | |
| D. | β射线与γ射线一样是电磁波,但穿透本领远比γ射线小 |
3. 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度-时间图象和y方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度-时间图象和y方向的位移-时间图象如图所示,下列说法正确的是( )
 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度-时间图象和y方向的位移-时间图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度-时间图象和y方向的位移-时间图象如图所示,下列说法正确的是( )| A. | 质点的初速度为7m/s | |
| B. | 质点所受的合外力为3N | |
| C. | 质点初速度的方向与合外力方向垂直 | |
| D. | 2s末质点速度大小为6m/s |
 如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求:
如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求: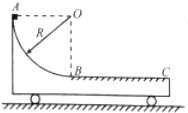 如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求:
如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求: