题目内容
7.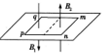 如图所示,将一质量为1kg、边长为1m的正方形导体框mnpq放在粗糙的绝缘水平面上,导体框的总电阻为0.25Ω,图中的虚线为该导体框的对称轴线,轴线的左侧(不包括pq边)存在竖直向下的磁场,磁感应强度大小随时间的变化规律为B1=t(T),轴线的右侧(包括mn边)存在竖直向上的磁感应强度大小为1T的匀强磁场.假设最大静摩擦力等于滑动摩擦力,导体框与水平面间的动摩擦因数为0.1,重力加速度g=10m/s2,则导体框释放的瞬间( )
如图所示,将一质量为1kg、边长为1m的正方形导体框mnpq放在粗糙的绝缘水平面上,导体框的总电阻为0.25Ω,图中的虚线为该导体框的对称轴线,轴线的左侧(不包括pq边)存在竖直向下的磁场,磁感应强度大小随时间的变化规律为B1=t(T),轴线的右侧(包括mn边)存在竖直向上的磁感应强度大小为1T的匀强磁场.假设最大静摩擦力等于滑动摩擦力,导体框与水平面间的动摩擦因数为0.1,重力加速度g=10m/s2,则导体框释放的瞬间( )| A. | mn边所受的安培力方向向左 | B. | 导体框所受的合力为零 | ||
| C. | 导体框中的感应电流大小为2A | D. | 导体框的加速度大小为2m/s2 |
分析 根据电磁感应定律求导线框中的感应电动势,由欧姆定律求出感应电流,根据楞次定律求感应电流的方向,根据安培力公式求安培力大小,根据牛顿第二定律求出导体框的加速度;
解答 解:C、轴线的左侧存在竖直向下的磁场,磁感应强度${B}_{1}^{\;}=t(T)$,磁感应强度的变化率$\frac{△{B}_{1}^{\;}}{△t}=1$T/s,感应电动势为:$E=\frac{△{B}_{1}^{\;}}{△{t}_{1}^{\;}}•\frac{{L}_{\;}^{2}}{2}=1×\frac{1}{2}=\frac{1}{2}V$,导线框中的感应电流大小为:$I=\frac{E}{R}=\frac{\frac{1}{2}V}{0.25Ω}=2A$,故C正确;
A、根据楞次定律,磁感应强度均匀增大,磁通量均匀增大,感应电流的磁场方向与原磁场方向相反,导体框中产生逆时针方向的感应电流,mn边的电流由n流向m,根据左手定则,mn边所受的安培力方向向右,故A错误;
BD、导体框所受的最大静摩擦力${f}_{m}^{\;}=μmg=0.1×10=1N$,MN边所受的安培力${F}_{安}^{\;}={B}_{2}^{\;}IL=1×2×1=2N$,根据牛顿第二定律$a=\frac{{F}_{安}^{\;}-f}{m}=\frac{2-1}{1}m/{s}_{\;}^{2}$=$1m/{s}_{\;}^{2}$,故BD错误;
故选:C
点评 考查法拉第电磁感应定律与闭合电路欧姆定律的内容,掌握楞次定律的应用,理解左手定则的内容,注意穿过线圈磁通量的磁场方向不同,则会出现相互抵消现象.

练习册系列答案
相关题目
18. 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标上,如图中的a、b、c所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标上,如图中的a、b、c所示,根据图线可知( )
 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标上,如图中的a、b、c所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标上,如图中的a、b、c所示,根据图线可知( )| A. | 反映Pr变化的图线是c | |
| B. | 电源电动势为8V | |
| C. | 电源内阻为2Ω | |
| D. | 当电流为0.5A时,外电路的电阻为2Ω |
19.关于自由落体运动,下列叙述中错误的是( )
| A. | 某段时间内的平均速度等于这段时间内的初速度和末速度之和的一半 | |
| B. | 在任意相等相邻时间内的位移差为恒量 | |
| C. | 在任意时刻,速度的变化快慢相同 | |
| D. | 在任意相等时间内,速度的变化量相等 |
16. 如图所示,物体A、B用细绳与轻弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦,现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )
如图所示,物体A、B用细绳与轻弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦,现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )
 如图所示,物体A、B用细绳与轻弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦,现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )
如图所示,物体A、B用细绳与轻弹簧连接后跨过滑轮.A静止在倾角为45°的粗糙斜面上,B悬挂着.已知质量mA=3mB,不计滑轮摩擦,现将斜面倾角由45°减小到30°,那么下列说法中正确的是( )| A. | 弹簧的弹力将增大 | B. | 物体A对斜面的压力将增大 | ||
| C. | 物体A受到的静摩擦力将减小 | D. | 物体A可能被拉动 |
19.若有一星球密度与地球密度相同,它表面的重力加速度是地球表面重力加速度的3倍,则该星球质量是地球质量的( )
| A. | 0.5倍 | B. | 3倍 | C. | 27倍 | D. | 9倍 |
16. 如图,两根平行光滑金属导轨固定在同一水平面内,其左端接有定值电阻R.Ox轴平行于金属导轨,在0≤x≤4m的空间区域内存在着垂直导轨平面向下的磁场,磁感应强度B随坐标x(以m为单位)的分布规律为B=0.8-0.2x(T).金属棒ab在外力作用下从x=0处沿导轨运动,金属棒始终与导轨垂直并接触良好,不计导轨和金属棒的电阻.设在金属棒从x1=1m经x2=2m到x3=3m的过程中,R的电功率保持不变,则金属棒( )
如图,两根平行光滑金属导轨固定在同一水平面内,其左端接有定值电阻R.Ox轴平行于金属导轨,在0≤x≤4m的空间区域内存在着垂直导轨平面向下的磁场,磁感应强度B随坐标x(以m为单位)的分布规律为B=0.8-0.2x(T).金属棒ab在外力作用下从x=0处沿导轨运动,金属棒始终与导轨垂直并接触良好,不计导轨和金属棒的电阻.设在金属棒从x1=1m经x2=2m到x3=3m的过程中,R的电功率保持不变,则金属棒( )
 如图,两根平行光滑金属导轨固定在同一水平面内,其左端接有定值电阻R.Ox轴平行于金属导轨,在0≤x≤4m的空间区域内存在着垂直导轨平面向下的磁场,磁感应强度B随坐标x(以m为单位)的分布规律为B=0.8-0.2x(T).金属棒ab在外力作用下从x=0处沿导轨运动,金属棒始终与导轨垂直并接触良好,不计导轨和金属棒的电阻.设在金属棒从x1=1m经x2=2m到x3=3m的过程中,R的电功率保持不变,则金属棒( )
如图,两根平行光滑金属导轨固定在同一水平面内,其左端接有定值电阻R.Ox轴平行于金属导轨,在0≤x≤4m的空间区域内存在着垂直导轨平面向下的磁场,磁感应强度B随坐标x(以m为单位)的分布规律为B=0.8-0.2x(T).金属棒ab在外力作用下从x=0处沿导轨运动,金属棒始终与导轨垂直并接触良好,不计导轨和金属棒的电阻.设在金属棒从x1=1m经x2=2m到x3=3m的过程中,R的电功率保持不变,则金属棒( )| A. | 在x1与x3处的电动势之比为1:3 | |
| B. | 在x1与x3处受到磁场B的作用力大小之比为3:1 | |
| C. | 从x1到x2与从x2到x3的过程中通过R的电荷量之比为5:3 | |
| D. | 从x1到x2与从x2到x3的过程中R产生的焦耳热之比为5:3 |
 如图所示,用伏安法测电阻R0的值时,M、N接在恒压电源上,当S接a时电压表示数10V,电流表示数0.2A;当S接b时,电压表示数12V,电流表示数0.15A,为了较准确地测定R0的值,S应接在b点,R0的真实值为70Ω.
如图所示,用伏安法测电阻R0的值时,M、N接在恒压电源上,当S接a时电压表示数10V,电流表示数0.2A;当S接b时,电压表示数12V,电流表示数0.15A,为了较准确地测定R0的值,S应接在b点,R0的真实值为70Ω. 足够长的木板A右端固定一挡板B,木板连同挡板的质量为M=6.0kg,木板位于光滑水平面上,现在a位置放有一小物块,其质量为m=2.0kg,小物块与木板间的动摩擦因数为μ=0.3,它们都处于静止状态,现使小物块以初速度v0=4.0m/s沿木板向前滑动,直到和挡板相撞,碰撞后小物块被弹回,最后小物块与木板保持相对静止,物块与挡板碰撞时间极短且无能量损失,求整个过程中系统损失的动能是多少?
足够长的木板A右端固定一挡板B,木板连同挡板的质量为M=6.0kg,木板位于光滑水平面上,现在a位置放有一小物块,其质量为m=2.0kg,小物块与木板间的动摩擦因数为μ=0.3,它们都处于静止状态,现使小物块以初速度v0=4.0m/s沿木板向前滑动,直到和挡板相撞,碰撞后小物块被弹回,最后小物块与木板保持相对静止,物块与挡板碰撞时间极短且无能量损失,求整个过程中系统损失的动能是多少?