题目内容
11.一高尔夫球爱好者从高为20m的高处以某一初速度将高尔夫球水平击出,高尔夫球在空中沿水平方向运动100m后,恰好落到球洞里,不计空气阻力的作用,重力加速度g取10m/s2.求:(1)高尔夫球在空中运动的时间和高尔夫球被击出时的水平速度大小;
(2)高尔夫球落入球洞前瞬间的速度大小.
分析 (1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出运动的时间,结合水平位移求出初速度的大小.
(2)根据速度时间公式求出竖直分速度,结合平行四边形定则求出小球落地时的速度大小.
解答 解:(1)设小球做平抛运动的时间为t,沿竖直方向有:h=$\frac{1}{2}g{t}^{2}$
代入数据解得:t=2.0s
设小球做平抛运动的初速度为v0,沿水平方向有:x=v0t
代入数据解得:v0=50 m/s
(2)小球落地时竖直方向的速度大小为:vy=gt=20m/s
小球落地时的速度大小为:$v=\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{5{0}^{2}+2{0}^{2}=}10\sqrt{29}$m/s
答:(1)小球在空中运动的时间为2s;被抛出时的速度大小为50m/s;
(2)小球落地时的速度大小为10$\sqrt{29}$m/s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如下表所示:
某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如下表所示:
(1)根据表中的数据在图a所示的坐标中作出a-F图象;
(2)图象的斜率的物理意义是小车及车中砝码总质量的倒数;
(3)图象(或延长线)与F轴的截距的物理意义是小车所受的阻力;
(4)小车和砝码的总质量为1.0 kg.
 某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如下表所示:
某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如下表所示:| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/(m•s-2) | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
(2)图象的斜率的物理意义是小车及车中砝码总质量的倒数;
(3)图象(或延长线)与F轴的截距的物理意义是小车所受的阻力;
(4)小车和砝码的总质量为1.0 kg.
2.“轨道康复者”是“垃圾”卫星的救星,被称为“太空110”,它可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命,假设“轨道康复者”的轨道半经为地球同步卫星轨道半径的五分之一,其运动方向与地球自转方向一致,轨道平面与地球赤道平面重合,下列说法正确的是( )
| A. | “轨道康复者”的速度是地球同步卫星速度的5倍 | |
| B. | “轨道康复者”的加速度是地球同步卫星加速度的25倍 | |
| C. | 站在赤道上的人用仪器观察到“轨道康复者”向西运动 | |
| D. | “轨道康复者”可在高轨道上加速,以实现对低轨道上卫星的拯救 |
19. 如图所示为某物体做直线运动的v-t图象.关于这个物体在前4s内运动情况的说法中正确的是( )
如图所示为某物体做直线运动的v-t图象.关于这个物体在前4s内运动情况的说法中正确的是( )
 如图所示为某物体做直线运动的v-t图象.关于这个物体在前4s内运动情况的说法中正确的是( )
如图所示为某物体做直线运动的v-t图象.关于这个物体在前4s内运动情况的说法中正确的是( )| A. | 物体始终朝同一方向运动 | |
| B. | 物体加速度不变,方向与初速度方向相反 | |
| C. | 物体在前2 s内做匀减速运动 | |
| D. | 4 s内物体的位移是4 m |
6.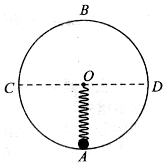 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )| A. | 当v0较小时,小球可能会离开圆轨道 | |
| B. | 若在$\sqrt{2gR}$<v0<$\sqrt{5gR}$则小球会在B、D间脱离圆轨道 | |
| C. | 只要v0>$\sqrt{4gR}$,小球就能做完整的圆周运动 | |
| D. | 只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差与v0无关 |
16.关于电源和电流,下列说法中正确的是( )
| A. | 电流是由大量电荷的无规则运动形成的 | |
| B. | 电路中只要有电源,就一定会有电流 | |
| C. | 在电源外部,电流从电源的正极流向负极 | |
| D. | 电流的方向总是从电源的正极流向负极 |
1.发现电流的磁效应的科学家是( )
| A. | 洛伦兹 | B. | 安培 | C. | 特斯拉 | D. | 奥斯特 |