题目内容
8. 如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:
如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:(1)若在玻璃砖左侧竖直放置一遮光板,使水平面BN不被照亮,遮光板的最小高度是多少?
(2)撤去遮光板,从OA的中点射入的光,在MN上的P处留下一个光点,P点到O点的距离是多少?
分析 (1)当光线射到AB面上恰好发生全反射时,遮光板的最小高度等于光线在AB面上的入射以ON的距离,根据折射定律求出临界角,由几何知识求出遮光板的最小高度.
(2)作出光路图,根据几何知识确定光线射到AB面上的入射角,由折射定律求出折射角,再由几何知识求出P点到O点的距离.
解答 解:(1)如图1,当光线在AB面入射角大于临界角C时,将没有光线出射后射向BN平面,设遮光板高度为h,则
由折射定律有:sinC=$\frac{1}{n}$,
由几何知识得h=RsinC
求得h=$\frac{R}{n}$.
(2)如图2,当光在AB面中点入射时,入射角为30°,设P点到O点的距离为S,
由折射定律$\frac{sinθ}{sin30°}=n$,
解得sinθ=$\frac{1}{2}n$,cosθ=$\frac{\sqrt{4-{n}^{2}}}{2}$,
在直角△OEP中,θ=30+γ
根据正弦定律有:$\frac{S}{sin(180°-θ)}=\frac{R}{sinγ}$,
因此S=R$\frac{sinθ}{sinγ}$=$R\frac{sinθ}{sin(θ-30°)}$=$R\frac{sinθ}{sinθcos30°-sin30°cosθ}$,
代入θ的正弦值和余弦值,求得P点到O点的距离S=$\frac{2nR}{\sqrt{3}n-\sqrt{4-{n}^{2}}}$.
答:(1)遮光板的最小高度是$\frac{R}{n}$;
(2)P点到O点的距离是$\frac{2nR}{\sqrt{3}n-\sqrt{4-{n}^{2}}}$.
点评 本题考查了几何光学的运用,对数学能力的要求较高,关键作出光路图,结合折射定律和几何关系综合求解.

练习册系列答案
相关题目
18.在南半球地磁场的竖直分量向上,飞机MH370最后在南印度洋消失,由于地磁场的作用,金属机翼上有电势差,设飞行员左方机翼末端处的电势为Φ1,右方机翼末端处的电势为Φ2,则在南印度洋飞行时( )
| A. | 若飞机从西往东飞,Φ1比Φ2高 | B. | 若飞机从东往西飞,Φ1比Φ2高 | ||
| C. | 若飞机从北往南飞,Φ2比Φ1低 | D. | 若飞机从南往北飞,Φ2比Φ1高 |
19. 一个物体沿着直线运动,其v-t图象如图所示,根据图象下列说法正确的有( )
一个物体沿着直线运动,其v-t图象如图所示,根据图象下列说法正确的有( )
 一个物体沿着直线运动,其v-t图象如图所示,根据图象下列说法正确的有( )
一个物体沿着直线运动,其v-t图象如图所示,根据图象下列说法正确的有( )| A. | t=0到t=2s内物体做初速度为零的匀加速直线运动 | |
| B. | t=6s到t=8s内物体做匀减速直线运动 | |
| C. | 在t=0到t=2s内,物体的加速度为1m/s2 | |
| D. | 在t=0到t=8s内,物体运动的位移为13m |
16.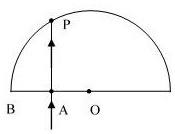 如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
 如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )| A. | 该玻璃对此单色光的折射率为1.5 | |
| B. | 光从 A 传到 P 的时间为$\frac{3R}{2c}$(c为空气中的光速) | |
| C. | 该玻璃对此单色光的临界角为45° | |
| D. | 玻璃的临界角随入射光线位置变化而变化 |
3.下列关于物理量的正、负号,理解正确的是( )
| A. | 加速度的正、负表示方向 | B. | 功的正、负表示方向 | ||
| C. | 重力势能的正、负表示方向 | D. | 电荷量的正、负表示方向 |
13. 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )| A. | 小球在圆周最低点时速度最大 | |
| B. | 小球在圆周最高点时细绳的拉力最小 | |
| C. | 小球圆周运动过程中细绳的拉力大小不变 | |
| D. | 小球圆周运动时细绳拉力的大小与小球质量无关 |
1.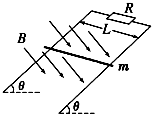 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )| A. | P=4mgv sinθ | |
| B. | P=2mgv sinθ | |
| C. | 当导体棒速度为$\frac{v}{2}$时加速度大小为$\frac{g}{2}$sinθ | |
| D. | 在速度达到2v以后匀速运动的过程中,R上产生的焦耳热等于拉力所做的功 |
2.两颗人造卫星绕地球做匀速圆周运动,质量之比为1:2,轨道半径之比为1:2,则( )
| A. | 线速度大小之比为1:$\sqrt{2}$ | B. | 运行的周期之比为1:2 | ||
| C. | 向心加速度大小之比为4:1 | D. | 它们的向心力大小之比为4:1 |
