题目内容
 质量为M的长方形木板静止在光滑水平面上,质量为m的小木块从木板的左端以初速度v0滑上木板,问木板至少多长小木块才不会从长方形木板上滑下?已知木板与小木块间的滑动摩擦系数为μ.
质量为M的长方形木板静止在光滑水平面上,质量为m的小木块从木板的左端以初速度v0滑上木板,问木板至少多长小木块才不会从长方形木板上滑下?已知木板与小木块间的滑动摩擦系数为μ.分析:木块滑上木板后,木块做匀减速直线运动,木板做匀加速直线运动,刚好不滑下的临界状态时速度相同时恰好到达另一端,结合动量守恒定律和能量守恒定律求出木板的长度.
解答:解:当两者速度相同时的速度为v,根据动量守恒定律得,
mv0=(M+m)v
解得v=
.
根据能量守恒定律得,
μmgL=
mv02-
(M+m)v2
解得:L=
.
答:木板至少长度为
,木块不会从长木板滑下.
mv0=(M+m)v
解得v=
| mv0 |
| M+m |
根据能量守恒定律得,
μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
解得:L=
| Mv02 |
| 2(M+m)μg |
答:木板至少长度为
| Mv02 |
| 2(M+m)μg |
点评:本题也可以根据木块和木板的运动规律,通过牛顿第二定律和运动学公式进行求解,但是没有动量守恒定律和能量守恒定律解决简捷.

练习册系列答案
相关题目
 如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )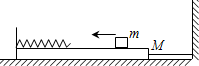 如图所示,质量为M的长方形木板静止在光滑水平面上,木板的左侧固定一劲度系数为k的轻质弹簧,木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上.绳所能承受的最大拉力为T.一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动,而后压缩弹簧.弹簧被压缩后所获得的弹性势能可用公式
如图所示,质量为M的长方形木板静止在光滑水平面上,木板的左侧固定一劲度系数为k的轻质弹簧,木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上.绳所能承受的最大拉力为T.一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动,而后压缩弹簧.弹簧被压缩后所获得的弹性势能可用公式