题目内容
甲、乙两质点同时开始在彼此平行且靠近的两水平轨道上同方向运动,甲在前,乙在后,相距s,甲初速度为零,加速度为a,做匀加速直线运动;乙以速度v0做匀速直线运动.关于两质点在相遇前的运动,某同学作如下分析:设两质点相遇前,它们之间的距离为Δs,则Δs=![]() at2+s-v0t,当t=
at2+s-v0t,当t=![]() 时,两质点间距离Δs有最小值,也就是两质点速度相等时,两质点之间距离最近.你觉得他的分析是否正确?如认为是正确的,请求出它们的最小距离;如认为是不正确的,请说明理由并作出正确的分析.
时,两质点间距离Δs有最小值,也就是两质点速度相等时,两质点之间距离最近.你觉得他的分析是否正确?如认为是正确的,请求出它们的最小距离;如认为是不正确的,请说明理由并作出正确的分析.
解析:不正确.在两质点相遇之前,它们之间的距离Δs也可能不断减小,直至Δs=0(相遇),而不存在先变小后变大的情况,这完全取决于两质点之间的初始距离s与v0、a之间的大小关系.由s=v0t-![]() at2可解得:t=
at2可解得:t= .可见,若v02=2as,即s=
.可见,若v02=2as,即s=![]() ,则t=
,则t=![]() .当t≤
.当t≤![]() 时,甲、乙之间的距离Δs始终在减小,直至相遇(最小距离Δs=0),不会出现Δs最小的情况.当v02<2as,即s>
时,甲、乙之间的距离Δs始终在减小,直至相遇(最小距离Δs=0),不会出现Δs最小的情况.当v02<2as,即s>![]() 时,甲与乙不可能相遇;两质点间距离会出现先变小后变大的情况;当t=
时,甲与乙不可能相遇;两质点间距离会出现先变小后变大的情况;当t=![]() 时,两质点之间的距离最近:Δsmin=s-
时,两质点之间的距离最近:Δsmin=s-![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 甲、乙两质点同时开始做直线运动,它们的位移x与时间t的图象如图所示,则( )
甲、乙两质点同时开始做直线运动,它们的位移x与时间t的图象如图所示,则( )| A、甲物体做匀加速直线运动,乙物体做曲线运动 | B、甲、乙两物体从同一地点出发 | C、当甲、乙两物体速度相同时,二者之间的距离为零 | D、当甲、乙两物体有两次相遇 |
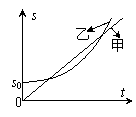
 甲、乙两质点同时开始做直线运动,它们的位移s与时间t的图象如图所示,则( )
甲、乙两质点同时开始做直线运动,它们的位移s与时间t的图象如图所示,则( )