��Ŀ����
13�� ��ͼ��ʾ��һ��ƽ��С����ֹ��ˮƽ�����ϣ�С��������M=3.0kg��ƽ�峵����L=l.0m��ƽ�峵���ϱ���������ĸ߶�H=0.8m��ijʱ�̣�һ������m=1.0kg��С��飨����Ϊ�ʵ㣩��v0=3.0m/s��ˮƽ�ٶȻ���С������ˣ����ͬʱ���С��ʩ��һ��F=15N��ˮƽ���ҵĺ����������С��֮��Ķ�Ħ��������=0.30������С���������Ħ�����������ٶ�gȡ10m/s2����
��ͼ��ʾ��һ��ƽ��С����ֹ��ˮƽ�����ϣ�С��������M=3.0kg��ƽ�峵����L=l.0m��ƽ�峵���ϱ���������ĸ߶�H=0.8m��ijʱ�̣�һ������m=1.0kg��С��飨����Ϊ�ʵ㣩��v0=3.0m/s��ˮƽ�ٶȻ���С������ˣ����ͬʱ���С��ʩ��һ��F=15N��ˮƽ���ҵĺ����������С��֮��Ķ�Ħ��������=0.30������С���������Ħ�����������ٶ�gȡ10m/s2������1��������С�����е������룻
��2��������ʱ�������С�����֮���ˮƽ���룮
���� ��1������ţ�ٵڶ����ɷֱ����������С��ʱ����С���ļ��ٶȣ�����ٶ���ȣ�����˶���ʱ�䣬����λ�ƹ�ʽ�������С����λ�ƣ��Ӷ��ó����ߵ����λ�ƣ�
��2���ٶ�����ܣ�������С������˻����Ĺ����У�����С�������ȼ���ֱ���˶�������ţ�ٵڶ����ɷֱ��������С���ļ��ٶȣ����λ�ƹ�ʽ�������黬��С��ʱС���ͻ�����ٶȣ����ţ�ٵڶ������������뿪С����С���ļ��ٶȣ������ƽ���˶������ݸ߶����ƽ���˶���ʱ�䣬ͨ���˶�ѧ��ʽ�������ˮƽλ���Լ�ƽ���˶�������С����λ�ƣ��Ӷ����������ʱ�������С�����֮���ˮƽ���룮
��� �⣺��1��������鲻���С���Ҷ˻����������黬��С��������ʱ��t1�������С���ﵽ��ͬ�ٶ�v1�����ʱ����������ȼ����˶���С�����ȼ���ֱ���˶���
����ţ�ٵڶ����ɵã����ļ��ٶ�${a}_{��1}=��g=3m/{s}^{2}$����������
С���ļ��ٶ�${a}_{��1}=\frac{F+��mg}{M}=\frac{15+0.3��10}{3}m/{s}^{2}$=6m/s2���������ң�
����v1=v0-a��1t1��=a��1t1��
�������ݽ��${t}_{1}=\frac{1}{3}s$��v1=2.0m/s��
��${x}_{��1}=\frac{{v}_{0}+{v}_{1}}{2}{t}_{1}=\frac{3+2}{2}��\frac{1}{3}m=\frac{5}{6}m$��
${x}_{��1}=\frac{{v}_{1}}{2}{t}_{1}=\frac{2}{2}��\frac{1}{3}m=\frac{1}{3}m$��
������С�����еľ����x1=x��1-x��1=0.5m��
��Ϊ��x1��L���������û�д�С���Ҷ˻������˺������ٶ�С��С�����ٶȣ������С��������˶�������������С�����е��������x1=0.5m��
��2��������С������˻����Ĺ����У�����С�������ȼ���ֱ���˶�������ţ�ٵڶ����ɵã�
���ļ��ٶ�${a}_{��2}=��g=3m/{s}^{2}$���������ң�
С���ļ��ٶ�${a}_{��2}=\frac{F-��mg}{M}=\frac{15-0.3��10}{3}m/{s}^{2}$=4m/s2���������ң�
���پ���ʱ��t2������˶���С������ˣ����ʱ���ڣ�����С����λ�Ʒֱ�Ϊ
${x}_{��2}={v}_{1}{t}_{2}+\frac{1}{2}{a}_{��2}{{t}_{2}}^{2}$��
${x}_{��2}={v}_{1}{t}_{2}+\frac{1}{2}{a}_{��2}{{t}_{2}}^{2}$��
����Ϊx��2-x��2=��x1��
�������ݽ��t2=1.0s��
��ʱv��2=v1+a��2t2=5m/s��
v��2=v1+a��2t2=6m/s��
��ʱ����С����˻��У���ƽ���˶���С�����ȼ���ֱ���˶�������ţ�ٵڶ����ɣ�
С���ļ��ٶ�${a}_{��3}=\frac{F}{M}=\frac{15}{3}m/{s}^{2}=5m/{s}^{2}$��
�������ƽ���˶���ʱ��Ϊt3��
H=$\frac{1}{2}g{{t}_{3}}^{2}$��
���t3=0.4s��
���ʱ���������ˮƽ�����λ��x��3=v��2t3=5��0.4m=2m��
С����λ��${x}_{��3}={v}_{��2}{t}_{3}+\frac{1}{2}{a}_{��3}{{t}_{3}}^{2}$��
�������ݽ��x��3=2.8m
����������ʱ�������С�����֮���ˮƽ�����x=x��3-x��3=2.8-2m=0.8m��
�𣺣�1��������С�����е�������Ϊ0.5m��
��2��������ʱ�������С�����֮���ˮƽ����Ϊ0.8m��
���� �������Ĺؼ�����ľ���ƽ�峵���˶����̣����ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮


| A�� | ����A���ȼ���ֱ���˶�������B������ֱ���˶� | |
| B�� | t2ʱ��AB����������ٶȷ����෴ | |
| C�� | 0-t1ʱ����A��λ�ƴ���B��λ�� | |
| D�� | t1ʱ��ǰA���ٶ�С��B���ٶ� |

| A�� | �����ӽ���ų������ʱ����0.15s | |
| B�� | �����ڵ糡���˶����ʱ����0.10s | |
| C�� | �����ڴų�����Բ���˶������뾶��0.5m | |
| D�� | �����ڴų����˶�������ٶ���v0��$\sqrt{2}$�� |
 ��ͼ��ʾΪ��ɡ�����߱��ݸ�¥��ɡ�����Σ����Ǵ�¥�����º��ھ����һ���߶ȴ���ɡ�������հ�ȫ��½������ɡ�ߣ�������
��ͼ��ʾΪ��ɡ�����߱��ݸ�¥��ɡ�����Σ����Ǵ�¥�����º��ھ����һ���߶ȴ���ɡ�������հ�ȫ��½������ɡ�ߣ�������| A�� | ��е��һֱ��С | B�� | ��е��һֱ���� | ||
| C�� | ����һֱ��С | D�� | ��������һֱ���� |
 ��ͼ��ʾ��һ��ԵϸԲ���뾶Ϊr���价��̶���ˮƽ���ϣ��糡ǿ��ΪE����ǿ�糡��Բ��ƽ��ƽ�У����ϴ���һ�����Ϊ+q������Ϊm��С����Բ������Ħ����Բ���˶�����С��A��ʱ�ٶ�vA�ķ���ǡ��糡��ֱ����Բ����С�����ˮƽ�������������ã����ٶ�vA=$\sqrt{\frac{qEr}{m}}$����С���˶�����A��ԳƵ�B��ʱ��С���Բ����ˮƽ�����������FB=6qE��
��ͼ��ʾ��һ��ԵϸԲ���뾶Ϊr���价��̶���ˮƽ���ϣ��糡ǿ��ΪE����ǿ�糡��Բ��ƽ��ƽ�У����ϴ���һ�����Ϊ+q������Ϊm��С����Բ������Ħ����Բ���˶�����С��A��ʱ�ٶ�vA�ķ���ǡ��糡��ֱ����Բ����С�����ˮƽ�������������ã����ٶ�vA=$\sqrt{\frac{qEr}{m}}$����С���˶�����A��ԳƵ�B��ʱ��С���Բ����ˮƽ�����������FB=6qE�� ��ͼ��ʾ�ڿռ��У�ֱ��MN���Ϸ��Ϸ����ڷ���ֱֽ���������ǿ�ų�����������Ȧabcd��a��������MN �غϣ���Ȧ��a����ʱ��������ת����һ������T�ڣ���Ȧ�в����ĸ�Ӧ����i��ʱ��t�仯��i-tͼ����ȷ���ǣ�������
��ͼ��ʾ�ڿռ��У�ֱ��MN���Ϸ��Ϸ����ڷ���ֱֽ���������ǿ�ų�����������Ȧabcd��a��������MN �غϣ���Ȧ��a����ʱ��������ת����һ������T�ڣ���Ȧ�в����ĸ�Ӧ����i��ʱ��t�仯��i-tͼ����ȷ���ǣ�������



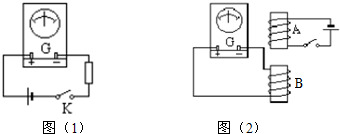
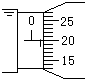 ��һ����˿��ֵ��100��-200��֮�䣬�����Ϊ0.25W�����÷�����ȷ����������ֵ��ʵ���ҳ��е��ߺ͵�������
��һ����˿��ֵ��100��-200��֮�䣬�����Ϊ0.25W�����÷�����ȷ����������ֵ��ʵ���ҳ��е��ߺ͵�������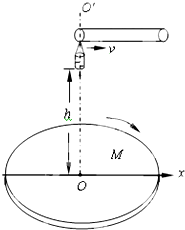 ��ͼ��ʾ��M��ˮƽ���õ�Բ�̣��ƹ���Բ�ĵ���ֱ��OO'����ת�����Ծ���Oˮƽ���ҵķ�����Ϊx�����������Բ��O���Ϸ��������Ϊh����һ�����ڼ�ϵ�ˮ����������t=0ʱ�̿�ʼ���㹻���Ĵ��ʹ�����x��ƽ�еķ���������ֱ���˶����ٶȴ�СΪv����֪������t=0ʱ���µ�һ��ˮ���Ժ�ÿ��ǰһ��ˮ�պ��䵽������ʱ�ٵ�һ��ˮ���ʣ�
��ͼ��ʾ��M��ˮƽ���õ�Բ�̣��ƹ���Բ�ĵ���ֱ��OO'����ת�����Ծ���Oˮƽ���ҵķ�����Ϊx�����������Բ��O���Ϸ��������Ϊh����һ�����ڼ�ϵ�ˮ����������t=0ʱ�̿�ʼ���㹻���Ĵ��ʹ�����x��ƽ�еķ���������ֱ���˶����ٶȴ�СΪv����֪������t=0ʱ���µ�һ��ˮ���Ժ�ÿ��ǰһ��ˮ�պ��䵽������ʱ�ٵ�һ��ˮ���ʣ�