题目内容
19. 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中,克服摩擦力做功为$\frac{1}{2}mgR$.
如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中,克服摩擦力做功为$\frac{1}{2}mgR$.
分析 根据向心力公式求出最高点的速度,由动能定理可以求出合外力做的功,可以求出克服摩擦力做的功
解答 解:小球到达B点刚好对轨道没有压力,根据牛顿第二定律有:
$mg=m\frac{{v}_{B}^{2}}{R}$
得:${v}_{B}^{\;}=\sqrt{gR}$
从P到B根据动能定理有:$mg(2R-R)-{W}_{克f}^{\;}=\frac{1}{2}m{v}_{B}^{2}-0$
代入数据得:${W}_{克f}^{\;}=\frac{1}{2}mgR$
故答案为:$\frac{1}{2}mgR$
点评 小球在B点对轨道没有压力,则小球做圆周运动的向心力由重力提供,摩擦力做功使物体的机械能减少,熟练应用动能定理即可正确解题.

练习册系列答案
相关题目
9.据《每日邮报》报道,科学家最新研究发现,在我们太阳系的早期可能存在过另外一颗行星,后来与海王星碰撞后离开了太阳系.海王星也由于受到撞击改变了轨道,假设海王星变轨前后的稳定轨道都可看作是圆周,碰撞后轨道半径变小,则海王星在新轨道上稳定运行与原轨道相比( )
| A. | 角速度变大 | B. | 线速度变小 | C. | 周期变大 | D. | 加速度变小 |
10. 跳伞员跳伞时,降落伞最初一段时间内并不张开,跳伞员做加速运动.随后,降落伞张开,跳伞员做减速运动,如图所示,降落伞的速度减小至一定值后便不再降低,跳伞员以这一速度做匀速运动,直至落地.无风时某跳伞员竖直下落,着地时速度是4m/s,若在水平方向有风,风力使他在水平方向有3m/s的分速度,则该跳伞员在匀速下落过程中( )
跳伞员跳伞时,降落伞最初一段时间内并不张开,跳伞员做加速运动.随后,降落伞张开,跳伞员做减速运动,如图所示,降落伞的速度减小至一定值后便不再降低,跳伞员以这一速度做匀速运动,直至落地.无风时某跳伞员竖直下落,着地时速度是4m/s,若在水平方向有风,风力使他在水平方向有3m/s的分速度,则该跳伞员在匀速下落过程中( )
 跳伞员跳伞时,降落伞最初一段时间内并不张开,跳伞员做加速运动.随后,降落伞张开,跳伞员做减速运动,如图所示,降落伞的速度减小至一定值后便不再降低,跳伞员以这一速度做匀速运动,直至落地.无风时某跳伞员竖直下落,着地时速度是4m/s,若在水平方向有风,风力使他在水平方向有3m/s的分速度,则该跳伞员在匀速下落过程中( )
跳伞员跳伞时,降落伞最初一段时间内并不张开,跳伞员做加速运动.随后,降落伞张开,跳伞员做减速运动,如图所示,降落伞的速度减小至一定值后便不再降低,跳伞员以这一速度做匀速运动,直至落地.无风时某跳伞员竖直下落,着地时速度是4m/s,若在水平方向有风,风力使他在水平方向有3m/s的分速度,则该跳伞员在匀速下落过程中( )| A. | 跳伞员着地速度的大小为5m/s | |
| B. | 跳伞员着地速度的方向与风速无关 | |
| C. | 跳伞员和降落伞受到的空气的作用力方向竖直向上 | |
| D. | 跳伞员和降落伞的机械能守恒 |
7.一质点开始时做匀速直线运动,从某时刻起受到一恒力作用.此后,该质点可能做( )
| A. | 匀速圆周运动 | B. | 变速圆周运动 | C. | 变加速直线运动 | D. | 匀变速曲线运动 |
14.有三个质量都是m的小球a、b、c,以大小相同的速度v0在空中同一点分別竖直向上、水平和斜向上抛出,三球运动描述正确的是(不计空气阻力)( )
| A. | 三球落地时动能相同 | B. | 三球落地时间相同 | ||
| C. | 三球落地时速度相同 | D. | 三球落地时机械能不同 |
11. 如图所示,在质量为M的小车中挂着一单摆,摆球质量为m0,小车和单摆以恒定的速度v沿光滑水平地面运动,与位于正前方的质量为m的静止的木块发生碰撞,碰撞的时间极短.在此碰撞过程中,下列情况可能发生的是( )
如图所示,在质量为M的小车中挂着一单摆,摆球质量为m0,小车和单摆以恒定的速度v沿光滑水平地面运动,与位于正前方的质量为m的静止的木块发生碰撞,碰撞的时间极短.在此碰撞过程中,下列情况可能发生的是( )
 如图所示,在质量为M的小车中挂着一单摆,摆球质量为m0,小车和单摆以恒定的速度v沿光滑水平地面运动,与位于正前方的质量为m的静止的木块发生碰撞,碰撞的时间极短.在此碰撞过程中,下列情况可能发生的是( )
如图所示,在质量为M的小车中挂着一单摆,摆球质量为m0,小车和单摆以恒定的速度v沿光滑水平地面运动,与位于正前方的质量为m的静止的木块发生碰撞,碰撞的时间极短.在此碰撞过程中,下列情况可能发生的是( )| A. | 小车、木块、摆球的速度都发生变化,分别变为v1、v2、v3,满足(M+m0)v=Mv1+mv2+m0v3 | |
| B. | 摆球的速度不变,小车和木块的速度变为v1和v2,满足Mv=Mv1+mv2 | |
| C. | 摆球的速度不变,小车和木块的速度都变为u,满足Mv=(M+m)u | |
| D. | 小车和摆球的速度都变为v1,木块的速度变为v2,满足(M+m0)v=(M+m0)v1+mv2 |
5. 如图质量为m的汽车在水平路面上启动,运动过程中的速度图象,Oa为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法正确的是( )
如图质量为m的汽车在水平路面上启动,运动过程中的速度图象,Oa为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法正确的是( )
 如图质量为m的汽车在水平路面上启动,运动过程中的速度图象,Oa为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法正确的是( )
如图质量为m的汽车在水平路面上启动,运动过程中的速度图象,Oa为过原点的倾斜直线,ab段表示以额定功率行驶时的加速阶段,bc段是与ab段相切的水平直线,则下述说法正确的是( )| A. | t1-t2时间内汽车牵引力做功为$\frac{1}{2}$m${{v}_{2}}^{2}$-$\frac{1}{2}$m${{v}_{1}}^{2}$ | |
| B. | 0-t1时间内汽车做匀加速运动且功率逐渐增大 | |
| C. | t2-t3时间内汽车的牵引力最小,与阻力相等 | |
| D. | t1-t2时间内汽车的牵引力逐渐在增大 |
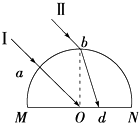 半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{3}$,求该玻璃砖的折射率.
半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{3}$,求该玻璃砖的折射率. 倾角θ=30o、长L=2.7m的斜面,底端与一个光滑的四分之一圆弧平滑连接,圆弧底端切线水平,一质量m=1kg的小滑块从斜面最高处的A点由静止沿斜面下滑,经过斜面底端B恰好到达圆弧轨道最高点C;又沿圆弧折返,恰好能到达斜面上的D点处,再从D点滑下,小滑块如此往复运动,最后停在B点,已知滑块与斜面间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$,g=10m/s2,求:
倾角θ=30o、长L=2.7m的斜面,底端与一个光滑的四分之一圆弧平滑连接,圆弧底端切线水平,一质量m=1kg的小滑块从斜面最高处的A点由静止沿斜面下滑,经过斜面底端B恰好到达圆弧轨道最高点C;又沿圆弧折返,恰好能到达斜面上的D点处,再从D点滑下,小滑块如此往复运动,最后停在B点,已知滑块与斜面间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$,g=10m/s2,求: