题目内容
1. 如图所示,质量为M的半球形绝缘体A放在粗糙水平地面上,通过最高点处的钉子用水平绝缘细线拉住一质量为m的光滑球B.A、B的球心连线与竖直方向成30°角,B均匀带正电,电荷量为q.A、B处在电场强度大小为E、方向与水平面成60°角斜向右下方的匀强电场中.A、B整体静止,己知重力加速度为g.则下列说法正确的是( )
如图所示,质量为M的半球形绝缘体A放在粗糙水平地面上,通过最高点处的钉子用水平绝缘细线拉住一质量为m的光滑球B.A、B的球心连线与竖直方向成30°角,B均匀带正电,电荷量为q.A、B处在电场强度大小为E、方向与水平面成60°角斜向右下方的匀强电场中.A、B整体静止,己知重力加速度为g.则下列说法正确的是( )| A. | A对地面的压力大小为($\frac{\sqrt{3}}{2}m+M$)g$+\frac{\sqrt{3}}{2}$qE | |
| B. | A对地面的摩檫力方向水平向左,大小为$\frac{1}{2}$qE | |
| C. | 细线对B的拉力大小为$\frac{\sqrt{3}}{3}$mg+qE | |
| D. | B对A的压力大小为$\frac{\sqrt{3}}{2}$mg+$\frac{1}{2}$qE |
分析 对选项AB,运用整体法,受力分析后根据平衡条件列式分析;对选项CD,隔离球B,受力分析后根据平衡条件列式分析.
解答 解:AB、对球和半球形绝缘体整体分析,受重力、支持力、电场力和摩擦力,根据平衡条件,有:
N=(M+m)g+qEsin60°=(M+m)g+$\frac{\sqrt{3}}{2}$qE;
f=qEcos60°=$\frac{1}{2}$qE,向左;
根据牛顿第三定律,A对地面的压力大小为(M+m)g+$\frac{\sqrt{3}}{2}$qE;A对地面的摩檫力方向水平向右,大小为$\frac{1}{2}$qE;故A错误,B错误;
CD、对球受力分析,受重力、支持力、拉力和电场力,如图所示:
根据平衡条件,有:
T=Nsin30°+qEsin30°
Ncos30°=mg+qEcos30°
联立解得:
T=$\frac{\sqrt{3}}{3}mg+qE$
N=$\frac{2\sqrt{3}}{3}mg+qE$
根据牛顿第三定律,压力为$\frac{2\sqrt{3}}{3}mg+qE$,故C正确,D错误;
故选:C.
点评 本题包含电场力的共点力平衡问题,关键是采用整体法和隔离法灵活选择研究对象,受力分析后根据平衡条件列式分析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.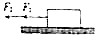 如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
 如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )| A. | $\frac{\sqrt{Pk}}{2m}$ | B. | $\frac{\sqrt{Pk}}{m}$ | C. | $\frac{3\sqrt{Pk}}{m}$ | D. | $\frac{4\sqrt{Pk}}{m}$ |
12. 在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
 在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )| A. | a光在玻璃砖内的频率比在空气中的小 | |
| B. | a光的频率比b光的小 | |
| C. | a光的折射率大于b光的折射率 | |
| D. | 在玻璃砖内a光的传播速度比c小 | |
| E. | 相同条件下进行双缝干涉实验,a光的条纹间距比b光的小 |
16. 如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光线Ⅰ、Ⅱ、Ⅲ,若平面镜的上下表面足够宽,下列说法正确的是( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光线Ⅰ、Ⅱ、Ⅲ,若平面镜的上下表面足够宽,下列说法正确的是( )
 如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光线Ⅰ、Ⅱ、Ⅲ,若平面镜的上下表面足够宽,下列说法正确的是( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光线Ⅰ、Ⅱ、Ⅲ,若平面镜的上下表面足够宽,下列说法正确的是( )| A. | 光束I仍为复色光,光束Ⅱ、Ⅲ为单色光 | |
| B. | 玻璃对光束Ⅲ的折射率大于对光束Ⅱ的折射率 | |
| C. | 改变α角,光线Ⅰ、Ⅱ、Ⅲ仍保持平行 | |
| D. | 通过相同的双缝干涉装置,光束Ⅱ产生的条纹宽度要大于光束Ⅲ的 | |
| E. | 在真空中,光束Ⅱ的速度要等于光束Ⅲ的速度 |

 如图所示,在球形烧瓶上连一根水平玻璃管,管中装有一小段水银柱把瓶中气体与外界的大气隔开,将烧瓶从室温情况下浸人热水中,可以看到此时水平玻璃管中的木银柱将向右移动(选填“向左”、“向右”或“不”).在这个实验中,烧瓶中气体初、末状态参量的变化是:压强不变,温度升高,体积增加.
如图所示,在球形烧瓶上连一根水平玻璃管,管中装有一小段水银柱把瓶中气体与外界的大气隔开,将烧瓶从室温情况下浸人热水中,可以看到此时水平玻璃管中的木银柱将向右移动(选填“向左”、“向右”或“不”).在这个实验中,烧瓶中气体初、末状态参量的变化是:压强不变,温度升高,体积增加. 如图所示,右端开口的绝缘、绝热圆柱形汽缸放置在水平地面上,容积为V,汽缸内部被绝热活塞M和导热性能良好的活塞N分成三个相等的部分,左边两部分分别封闭气体A和B,两活塞均与汽缸接触良好,忽略一切摩擦,汽缸左边有加热装置,可对气体A缓慢加热,初始状态温度为T0,大气压强为P0
如图所示,右端开口的绝缘、绝热圆柱形汽缸放置在水平地面上,容积为V,汽缸内部被绝热活塞M和导热性能良好的活塞N分成三个相等的部分,左边两部分分别封闭气体A和B,两活塞均与汽缸接触良好,忽略一切摩擦,汽缸左边有加热装置,可对气体A缓慢加热,初始状态温度为T0,大气压强为P0