题目内容
如图所示,ABDO是固定在竖直平面内的光滑轨道,AB是半径为R=15 m的四分之一圆周轨道,半径OA处于水平位置,BDO是直径为15 m的半圆轨道,D为BDO轨道的中央.AB和BDO相切于B点.一个小球P从A点的正上方距水平半径OA高H处自由落下,沿竖直平面内的轨道通过D点时对轨道的压力大小等于其重力大小的![]() 倍.取g=10m/
倍.取g=10m/![]() .
.
(1)求高度H;
(2)试讨论此球能否到达BDO轨道的最高点O;
(3)求小球沿轨道运动后再次落到轨道上的速度大小.

(1)10m (2)能够通过最高点 (3)10![]() m/s
m/s
解析:
(1)小球从H高处落下,进入轨道,沿BOD轨道做圆周运动,小球受重力和轨道的支持力. (设小球在D点时的速度为v,通过D点时轨道对小球的支持力等于(大小等于小球对轨道的压力)它做圆周运动的向心力,即
![]() ………..①(2分)
………..①(2分)
小球从P点落下直到沿光滑轨道运动的过程中,机械能守恒,有
![]() ………..②(2分)
………..②(2分)
由①②式可解得高度![]() ………..(2分)
………..(2分)
(2)设小球能够沿竖直半圆轨道运动到O点的最小速度为![]() ,有
,有
![]() ………..③(1分)
………..③(1分)
设小球至少应从![]() 高处落下,
高处落下,
![]() ………..④(1分)
………..④(1分)
由③④可得![]()
由![]() ,小球可以通过最高点. ………..(2分)
,小球可以通过最高点. ………..(2分)
(3)小球由H高落下通过O点的速度为![]() ………(2分)
………(2分)
小球通过O点后做平抛运动,设小球经过时间t落到AB圆弧轨道上,建立坐标系
![]() ………..⑤(1分)
………..⑤(1分)
![]() ………..⑥(1分)
………..⑥(1分)
又由几何关系![]() ………..⑦(1分)
………..⑦(1分)
由⑤⑥⑦可解得时间![]() (另解舍去)
(另解舍去)
小球落到轨道上的速度的大小为![]() (2分)
(2分)

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 如图所示,ABDO是处于竖直平面的光滑轨道,AB是半径为R=15m的1/4圆周轨道,半径OA处于水平位置,BDO是直径为15m的半圆轨道.一个小球P从A点的正上方距水平半径OA高H处自由落下,由A点进入竖直平面内的轨道,当小球通过最高点O时,小球与轨道间作用力为重力的5/3倍.取g=10m/s2.求:
如图所示,ABDO是处于竖直平面的光滑轨道,AB是半径为R=15m的1/4圆周轨道,半径OA处于水平位置,BDO是直径为15m的半圆轨道.一个小球P从A点的正上方距水平半径OA高H处自由落下,由A点进入竖直平面内的轨道,当小球通过最高点O时,小球与轨道间作用力为重力的5/3倍.取g=10m/s2.求: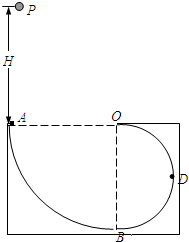 (2006?东城区一模)如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的
(2006?东城区一模)如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的 如图所示,ABDO是处于竖直平面内的固定光滑轨道,AB是半径为R=15m的
如图所示,ABDO是处于竖直平面内的固定光滑轨道,AB是半径为R=15m的 如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的
如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的