题目内容
12.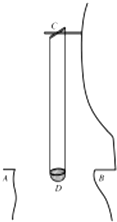 图中A、B之间为一峡谷,相距d=10.0m,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量M=200kg,每根绳的长度都是l=50.0m,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m=2.00kg的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆到A处时,他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小v0=4.0m/s,方向都是水平的,试求:
图中A、B之间为一峡谷,相距d=10.0m,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量M=200kg,每根绳的长度都是l=50.0m,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m=2.00kg的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆到A处时,他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小v0=4.0m/s,方向都是水平的,试求:(1)此人需向箩筐中扔的石块数.
(2)从扔出第一个石块起到此人到达B处所经过的时间.
分析 (1)石块扔入箩筐的过程,水平方向动量守恒,根据动量守恒定律列式,得到当第n个石块进入筐时筐的速度vn的表达式.若箩筐具有速度vn后,恰好能摆到峡谷的A处,此时,筐上升的高度为h,由几何关系求出h,再由能量关系求石块数n.
(2)由运动学公式求从抛出第一个石块到石块进入箩筐经历的时间t1.箩筐摆动经历一个周期T,第二个石块进入筐,经历2个周期即2T,第三个石块进入筐,…,从第一个石块进入筐至第n个石块进入筐共经历时间为t2=(n-1)T,自第n个石块进入筐到筐摆到A处,人跨入筐所经历的时间为t3=$\frac{3}{4}$T,从人跨入筐到筐摆到B处经历时间为t4=$\frac{1}{4}$T,再求总时间t.
解答 解:(1)设第一个石块扔入箩筐后,筐开始运动的速度为v1,取水平向右为正方向,由动量守恒定律有:
mv0=(M+m)v1 …①
解得:v1=$\frac{m{v}_{0}}{M+m}$…②
当第二个石块刚要进箩筐时,箩筐恰好刚回到峡谷中央,速度的大小为v1,方向与石块速度v0的方向相同,设石块进入筐后,筐的速度为v2,由动量守恒定律有
mv0+(M+m)v1=(M+2m)v2 …③
由②③两式,得 v2=$\frac{2m{v}_{0}}{M+2m}$…④
当第n个石块进入筐时,筐的速度为 vn=$\frac{nm{v}_{0}}{M+nm}$…⑤
若箩筐具有速度Vn后,恰好能摆到峡谷的A处,此时,筐上升的高度为h,则由能量关系得:
$\frac{1}{2}(M+nm){v}_{n}^{2}$=(M+nm)gh…⑥
而:h=l-$\sqrt{{l}^{2}-\frac{1}{4}{d}^{2}}$…⑦
解⑤、⑥、⑦式得:n=$\frac{M\sqrt{2g(l-\sqrt{{l}^{2}-\frac{1}{4}{d}^{2}})}}{m[{v}_{0}-\sqrt{2g(l-\sqrt{{l}^{2}-\frac{1}{4}{d}^{2}})}]}$…⑧
代入数据,得:n=128…⑨即需向箩筐中扔进128个石块.
(2)从抛出第一个石块到石块进入箩筐经历的时间为:t1=$\frac{\frac{1}{2}d}{{v}_{0}}$…⑩
箩筐摆动经历一个周期T,第二个石块进入筐,经历2个周期即2T,第三个石块进入筐,…,从第一个石块进入筐至第n个石块进入筐共经历时间为:
t2=(n-1)T…(11)
自第n个石块进入筐到筐摆到A处,人跨入筐所经历的时间 t3=$\frac{3}{4}$T…(12)
从人跨入筐到筐摆到B处经历时间为:t4=$\frac{1}{4}$T…(13)
由此得自扔出第一个石块到此人到达B处总共需时间为:
t=t1+t2+t3+t4=$\frac{d}{2{v}_{0}}$+(n+$\frac{1}{4}$)T…(14)
注意到筐摆动的周期为:T=2π$\sqrt{\frac{l}{g}}$…(15)
代入数据得:t=1798.7s≈29.9min
答:(1)此人需向箩筐中扔的石块数是128.
(2)从扔出第一个石块起到此人到达B处所经过的时间是29.9min.
点评 本题是周期性问题,分析清楚石块和筐的速度,采用归纳法得到速度的表达式是解题的关键.要抓住单摆的周期性,不能漏解.

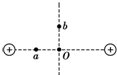 如图,等量同种正点电荷形成的静电场中,O是两点电荷连线的中点,a和b分别是连线上及中垂线上的点,且Oa=Ob,则以下说法中正确的是( )
如图,等量同种正点电荷形成的静电场中,O是两点电荷连线的中点,a和b分别是连线上及中垂线上的点,且Oa=Ob,则以下说法中正确的是( )| A. | 两点电荷连线上各点中O点处的电场强度为零,电势最低 | |
| B. | 从O点到b点处,电势降低,电场强度可能先增大后减小 | |
| C. | 负检验电荷从O点移到a点处加速度变大,电势能增加 | |
| D. | 正检验电荷分别从a点移到b点处和从a点移到O点处电场力做功一样多 |
| A. | 合运动一定指物体的实际运动 | |
| B. | 合运动的时间比分运动的时间长 | |
| C. | 合运动与分运动的位移、速度、加速度的关系都一定满足平行四边形定则 | |
| D. | 合运动与分运动是相对来说的,可以相互转化 |
| A. | 3.5 m | B. | 2 m | C. | 1 m | D. | 0 |
| A. | 40 N | B. | 140 N | C. | 240 N | D. | 400 N |
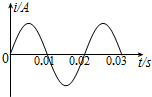 一个闭合矩形线在匀强磁场中绕垂直于磁感线的轴匀速转动,产生的感应电流如图所示.可得出的正确判断是( )
一个闭合矩形线在匀强磁场中绕垂直于磁感线的轴匀速转动,产生的感应电流如图所示.可得出的正确判断是( )| A. | t=0时刻,线圈平面与中性面垂直 | B. | t=0.01s时刻,磁通量最大 | ||
| C. | 该交变电流的频率为50Hz | D. | 该线圈转动角速度为100πrad/s |
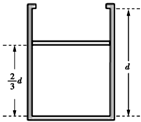 如图所示,圆柱形气缸的上部有小挡板,可以阻止活塞滑离气缸,气缸内部的高度为d,质量不计的薄活塞将一定质量的气体封闭在气缸内.开始时活塞离底部高度为$\frac{2}{3}$d,温度为t1=27℃,外界大气压强为p0=1atm,现对气体缓缓加热.求:
如图所示,圆柱形气缸的上部有小挡板,可以阻止活塞滑离气缸,气缸内部的高度为d,质量不计的薄活塞将一定质量的气体封闭在气缸内.开始时活塞离底部高度为$\frac{2}{3}$d,温度为t1=27℃,外界大气压强为p0=1atm,现对气体缓缓加热.求: