题目内容
1.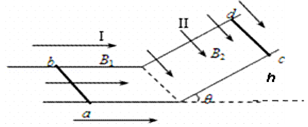 如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.
如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.(1)求导体棒cd沿斜轨道下滑的最大速度的大小;
(2)若已知从开始运动到cd棒达到最大速度的过程中,ab棒产生的焦耳热Q=0.45J,求该过程中通过cd棒横截面的电荷量;
(3)若已知cd棒开始运动时距水平轨道高度h=10m,cd棒由静止释放后,为使cd棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,试求cd棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B随时间t变化的关系式.
分析 由左、右手定则知道,当cd棒下滑时产生由d向c的电流,而ab棒受到竖直向下的安培力,这样ab棒始终静止在水平轨道上.
(1)下滑过程中当cd受到的合力为零时,速度达到最大,结合E=BLv,欧姆定律、安培力公式代入平衡条件就能求出最大速度.
(2)由能量守恒定律可以求出减少的机械能,从而减少的重力势能求出,下滑的距离x也求出,磁通量的变化量求出,用平均值方法求出电荷量.
(3)由于cd中无感应电流,则不受安培力,所以cd以gsinθ的加速度下滑,从而下滑的距离表达式可以写出来,由于△∅=0,所以先表示出初始状态的磁通量,再表示出经过t后的磁通量,两者相等,就能写出B随时间t的关系式.
解答 解:(1)cd棒匀速运动时速度最大,设为vm,棒中感应电动分为E,电流为I,则
E=BLvm,$I=\frac{E}{2R}$
由平衡条件得:mgsinθ=BIL
代入数据解得:vm=1m/s
(2)设cd从开始运动到达最大速度的过程中,经过的时间为t,通过的距离为x,cd棒中平均感应电动势E1,
平均电流为I1,通过cd棒横截面的电荷量为q,由能守恒定律得:
$mgxsinθ=\frac{1}{2}m{{v}_{m}}^{2}+2Q$,
代入得到x=1m,
所以通过cd棒的电荷量:
$q={I}_{1}t=\frac{{E}_{1}}{2R}t=\frac{\frac{{B}_{2}Lx}{t}}{2R}t=\frac{{B}_{2}Lx}{2R}=\frac{1×1×1}{2×0.5}$=1C
(3)设cd棒开始运动时穿过回路的磁通量为∅0,cd棒在倾斜轨道上下滑的过程中,设加速大小为a,
经过时间t通过的距离为x1,穿过回路的磁通量为Φ,cd棒在倾斜轨道上下滑时间为t0,则:
∅0=${B}_{0}L\frac{h}{sinθ}$
加速度:a=gxinθ
位移:${x}_{1}=\frac{1}{2}a{t}^{2}$
而 Φ=$BL(\frac{h}{sinθ}-{x}_{1})$
当cd棒下滑到最低点时有:
$\frac{h}{sinθ}=\frac{1}{2}a{{t}_{0}}^{2}$
解得:${t}_{0}=\sqrt{8}s$
为使cd棒中无感应电流,必须有:∅0=Φ
解得$B=\frac{8}{8-{t}^{2}}$ ($t<\sqrt{8}s$ )
答:(1)导体棒cd沿斜轨道下滑的最大速度的大小为1m/s.
(2)若已知从开始运动到cd棒达到最大速度的过程中,ab棒产生的焦耳热Q=0.45J,该过程中通过cd棒横截面的电荷量为1C.
(3)若已知cd棒开始运动时距水平轨道高度h=10m,cd棒由静止释放后,为使cd棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,cd棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B随时间t变化的关系式为$B=\frac{8}{8-{t}^{2}}$ ($t<\sqrt{8}s$ ).
点评 本题要注意的是:①看起来是双杆问题,但由于ab受到向下的安培力,则ab始终静止,实际是单杆问题.②cd下滑又要求无感应电流,则任意时间t回路的磁通量相等,分别表示出初、末状态的磁通量,则B随时间t的关系式就能求出.

| A. | 1 N | B. | 0.1 N | C. | 10 N | D. | 100 N |
 某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )| A. | a的电阻大于d的电阻 | B. | b的电阻大于c的电阻 | ||
| C. | c的电阻大于d的电阻 | D. | d的电阻大于a的电阻 |
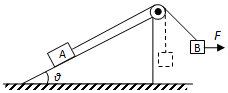 斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )
斜面放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,一水平力F作用于B上,整个系统处于静止状态,如图所示.现保持F方向不变,使B缓慢地移动到滑轮的正下方,该过程中A与斜面始终保持静止,在此过程中( )| A. | 斜面对物块A的摩擦力一直减小 | B. | 绳对滑轮的作用力保持不变 | ||
| C. | 地面对斜面的摩擦力一直减小 | D. | 地面对斜面的支持力保持不变 |
| A. | 库仑发现了电流的磁效应 | |
| B. | 麦克斯韦建立了完整的电磁场理论并首先验证了电磁波存在 | |
| C. | 法拉第发现了磁场产生电流的条件和规律 | |
| D. | 伽利略提出的万有引力定律奠定了天体力学的基础 |
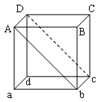 如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )
如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )| A. | $\frac{L}{2}$ | B. | $\frac{\sqrt{2}L}{2}$ | C. | $\frac{(2-\sqrt{2})L}{2}$ | D. | 以上答案都不对 |
 一个物体沿直线运动,从t=0 时刻开始,物体的$\frac{x}{t}$-t图象如图所示,试请求解物体运动5s后的位移及速度各多少?
一个物体沿直线运动,从t=0 时刻开始,物体的$\frac{x}{t}$-t图象如图所示,试请求解物体运动5s后的位移及速度各多少?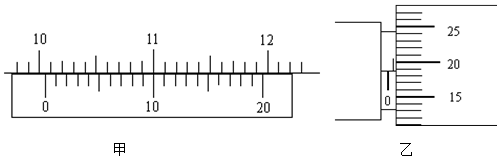
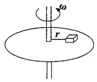 如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求:
如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求: