题目内容
1. 如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )
如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )| A. | 2$\sqrt{5}$m/s | B. | 2$\sqrt{15}$m/s | C. | 4$\sqrt{5}$m/s | D. | $\frac{4}{3}$$\sqrt{15}$m/s |
分析 根据竖直高度差求平抛运动的时间,再求竖直分速度,最后根据矢量三角形求合速度.
解答  解:根据$h=\frac{1}{2}g{t}_{\;}^{2}$得$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1}{10}}=\sqrt{\frac{1}{5}}s$
解:根据$h=\frac{1}{2}g{t}_{\;}^{2}$得$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1}{10}}=\sqrt{\frac{1}{5}}s$
竖直分速度:${v}_{y}^{\;}=gt=10×\sqrt{\frac{1}{5}}=\sqrt{20}m/s$
刚要落到球拍上时速度大小$v=\frac{{v}_{y}^{\;}}{cos60°}=\frac{\sqrt{20}}{\frac{1}{2}}=4\sqrt{5}m/s$,C正确,ABD错误
故选:C
点评 本题考查平抛运动的处理方法,平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,一定要记住平抛运动的规律.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
13.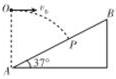 如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
 如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )| A. | 小球在空中飞行的时间为2s | |
| B. | 小球到达P点时速度为10 m/s | |
| C. | 小球到达P点时重力的功率为100W | |
| D. | 小球整个运动过程中速度的增加量为(2$\sqrt{29}$-4)m/s |
16.下列物理量中属于矢量的是( )
| A. | 功 | B. | 时间 | C. | 电场强度 | D. | 动能 |
 某探究学习小组的同学欲“探究小车动能变化与合外力对它做功的关系”,在实验室设计了一套如图所示的装置,图中A为小车,B为打点计时器,C为弹簧测力计,P为小桶(内有沙子),M是一端带有定滑轮的足够长水平放置的木板.要顺利完成该实验,除图中实验仪器和低压交流电源(含导线、纸带)外,还需要的两个实验仪器是刻度尺、天平.
某探究学习小组的同学欲“探究小车动能变化与合外力对它做功的关系”,在实验室设计了一套如图所示的装置,图中A为小车,B为打点计时器,C为弹簧测力计,P为小桶(内有沙子),M是一端带有定滑轮的足够长水平放置的木板.要顺利完成该实验,除图中实验仪器和低压交流电源(含导线、纸带)外,还需要的两个实验仪器是刻度尺、天平.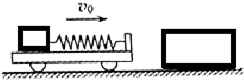 如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:
如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求: 小明同学看到一个纽扣锂电池标称电动势为3V,内阻约为1kΩ.为了较准确测定其电动势和内阻,除待测电池外,还备有如下器材:
小明同学看到一个纽扣锂电池标称电动势为3V,内阻约为1kΩ.为了较准确测定其电动势和内阻,除待测电池外,还备有如下器材: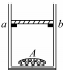 如图所示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60cm处设有a、b两限制装置,使活塞只能向上滑动.开始时活塞搁在a、b上,缸内气体的压强为1.0×105Pa,温度为300K.现缓慢加热汽缸内气体,当温度为330K时,活塞恰好离开a、b;当温度为360K时,活塞上升了4cm,取g=10m/s2,大气压强为1.0×105Pa.求活塞的质量和物体A的体积.
如图所示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60cm处设有a、b两限制装置,使活塞只能向上滑动.开始时活塞搁在a、b上,缸内气体的压强为1.0×105Pa,温度为300K.现缓慢加热汽缸内气体,当温度为330K时,活塞恰好离开a、b;当温度为360K时,活塞上升了4cm,取g=10m/s2,大气压强为1.0×105Pa.求活塞的质量和物体A的体积.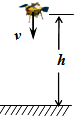 如图所示,“嫦娥三号”探测器在月球上着陆的最后阶段为:当探测器下降到距离月球表面高度为h时,探测器速度竖直向下,大小为v,此时关闭发动机,探测器仅在重力(月球对探测器的重力)作用下落到月面.已知从关闭发动机到探测器着地时间为t,月球半径为R且h<<R,引力常量为G,忽略月球自转影响,则:
如图所示,“嫦娥三号”探测器在月球上着陆的最后阶段为:当探测器下降到距离月球表面高度为h时,探测器速度竖直向下,大小为v,此时关闭发动机,探测器仅在重力(月球对探测器的重力)作用下落到月面.已知从关闭发动机到探测器着地时间为t,月球半径为R且h<<R,引力常量为G,忽略月球自转影响,则: 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为$\frac{\sqrt{3}}{3}$mg. 在改变电场强度的大小和方向后,小球A的平衡位置在α=60°处,然后再将A的质量改变为2m,其新的平衡位置在α=30°处,A受到的电场力大小为mg.
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为$\frac{\sqrt{3}}{3}$mg. 在改变电场强度的大小和方向后,小球A的平衡位置在α=60°处,然后再将A的质量改变为2m,其新的平衡位置在α=30°处,A受到的电场力大小为mg.