题目内容
3.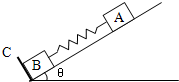 如图,在倾角为θ的光滑斜面上,有两个用轻质弹簧相连接的物体A、B.它们的质量均为m,弹簧的劲度系数k,C为一固定挡板.系统处一静止状态.现给A一个沿斜面向上的初速度v0,使A开始向上运动,当B刚要离开C时,A的速度多大?
如图,在倾角为θ的光滑斜面上,有两个用轻质弹簧相连接的物体A、B.它们的质量均为m,弹簧的劲度系数k,C为一固定挡板.系统处一静止状态.现给A一个沿斜面向上的初速度v0,使A开始向上运动,当B刚要离开C时,A的速度多大?
分析 先分析开始时及B刚要离开C时弹簧的状态,由胡克定律求出开始时弹簧的压缩量及B刚要离开C时弹簧的伸长量,从而得到物体A的位移.对系统,利用机械能守恒定律求当B刚要离开C时A的速度.
解答 解:令x1表示未加F时弹簧的压缩量,对A,由胡克定律和共点力平衡条件可知
mgsinθ=kx1
令x2表示B刚要离开C时弹簧的伸长量,对B,由胡克定律和平衡条件可知
kx2=mgsinθ
可得 x1=x2=$\frac{mgsinθ}{k}$
则此过程中A上升的位移 d=x1+x2=$\frac{2mgsinθ}{k}$
对A、B及弹簧组成的系统,只有重力和弹力做功,系统的机械能守恒,由于初末弹簧的弹性势能相等,则有
$\frac{1}{2}m{v}_{0}^{2}$=mgdsinθ+$\frac{1}{2}m{v}^{2}$
解得当B刚要离开C时,A的速度为 v=$\sqrt{{v}_{0}^{2}-\frac{4m{g}^{2}si{n}^{2}θ}{k}}$
答:当B刚要离开C时,A的速度为$\sqrt{{v}_{0}^{2}-\frac{4m{g}^{2}si{n}^{2}θ}{k}}$.
点评 本题关键要多次对物体A和B受力分析,求出弹簧的弹力,最后再根据系统的机械能守恒解答.

练习册系列答案
相关题目
3.对能量耗散的理解,下列说法中正确的是( )
| A. | 能量在转化过程中变少的现象叫能量耗散 | |
| B. | 能量耗散表明能量在转化过程中是不守恒的 | |
| C. | 能量在转化后全部都成为我们不能利用的内能,这种现象叫能量耗散 | |
| D. | 能量在转化过程中守恒,从便于利用的变成了不便于利用的现象叫能量耗散 |
18. 如图所示菱形abcd的边长为$2\sqrt{3}$m,∠bad=60°,已知匀强电场的电场线平行于菱形abcd所在的平面,一个带电量q=-2×10-6C的点电荷由a点移动到c点的过程中,电势能增加了1.2×10-5J,由c点移动到b点的过程中电场力做功6×10-6J,则下列说法正确的是( )
如图所示菱形abcd的边长为$2\sqrt{3}$m,∠bad=60°,已知匀强电场的电场线平行于菱形abcd所在的平面,一个带电量q=-2×10-6C的点电荷由a点移动到c点的过程中,电势能增加了1.2×10-5J,由c点移动到b点的过程中电场力做功6×10-6J,则下列说法正确的是( )
 如图所示菱形abcd的边长为$2\sqrt{3}$m,∠bad=60°,已知匀强电场的电场线平行于菱形abcd所在的平面,一个带电量q=-2×10-6C的点电荷由a点移动到c点的过程中,电势能增加了1.2×10-5J,由c点移动到b点的过程中电场力做功6×10-6J,则下列说法正确的是( )
如图所示菱形abcd的边长为$2\sqrt{3}$m,∠bad=60°,已知匀强电场的电场线平行于菱形abcd所在的平面,一个带电量q=-2×10-6C的点电荷由a点移动到c点的过程中,电势能增加了1.2×10-5J,由c点移动到b点的过程中电场力做功6×10-6J,则下列说法正确的是( )| A. | c、b两点的电势差Ucb=3V | |
| B. | a点的电势高于c点的电势 | |
| C. | 负电荷由b点移到a点的过程中,电势能增加 | |
| D. | 该电场的场强为1V/m |
8. 图为一头大一头小的导体周围等势面和电场线(带有箭头为电场线)示意图,已知两个相邻等势面间的电势差相等,则( )
图为一头大一头小的导体周围等势面和电场线(带有箭头为电场线)示意图,已知两个相邻等势面间的电势差相等,则( )
 图为一头大一头小的导体周围等势面和电场线(带有箭头为电场线)示意图,已知两个相邻等势面间的电势差相等,则( )
图为一头大一头小的导体周围等势面和电场线(带有箭头为电场线)示意图,已知两个相邻等势面间的电势差相等,则( )| A. | a点和d点的电场强度一定相同 | |
| B. | a点的电势可能等于b点的电势 | |
| C. | 将负电荷从c点沿任意路线移到d点的过程中,电场力不做功 | |
| D. | 将正电荷从c点沿虚线移到e点,电势能先增大后减小 |
12.在《验证机械能守恒定律》的实验中,下面叙述正确的是( )
| A. | 应用天平称出重物的质量 | |
| B. | 应当选用点迹清晰,第一、二两点距离约2mm的纸带进行测量 | |
| C. | 操作时应先放纸带,后接通电源 | |
| D. | 打点计时器应接在电压为4~6V的直流电源上 |
13.如图所示为某示波管内的聚焦电场,实线和虚线分别表示电场线和等势线则( )

| A. | 场强 Ea>Eb,Eb>Ec | |
| B. | 电势 φa>φb,φc>φb | |
| C. | 沿 cba 路径移动质子与电子,电荷的电势能改变是一样的 | |
| D. | 沿 bc 方向直线射入的电子有可能做曲线运动 |
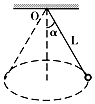 长为L的轻质细线,拴一质量为m的小球,一端固定于O点,让小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,已知摆线与竖直方向的夹角是α,求:
长为L的轻质细线,拴一质量为m的小球,一端固定于O点,让小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,已知摆线与竖直方向的夹角是α,求: 小明发现家里有一把玩具弹簧手枪,他想利用科技活动小组的仪器测出玩具手枪发出的钢珠的初速度.实验装置如图.右侧为一半径为R=0.4m的半圆形竖直轨道.在轨道的最低点和最高点分别安装有压力传惑器.他将一个质量为M,中心带沟槽的小木块静止放在圆轨道最低点,此时压力传感器Ⅰ显示示数为F0=1N.小明将枪口对准沟槽发射一颗质量为m=20g的小钢珠并嵌入沟槽内.钢珠嵌入瞬间压力传感器Ⅰ显示示数为F1=12N.小木块冲到圆轨道最高点时压力传感器2显示示数为F2=1.5N,由以上数据回答下面的问题.(不计空气阻力,取g=10m/s2)
小明发现家里有一把玩具弹簧手枪,他想利用科技活动小组的仪器测出玩具手枪发出的钢珠的初速度.实验装置如图.右侧为一半径为R=0.4m的半圆形竖直轨道.在轨道的最低点和最高点分别安装有压力传惑器.他将一个质量为M,中心带沟槽的小木块静止放在圆轨道最低点,此时压力传感器Ⅰ显示示数为F0=1N.小明将枪口对准沟槽发射一颗质量为m=20g的小钢珠并嵌入沟槽内.钢珠嵌入瞬间压力传感器Ⅰ显示示数为F1=12N.小木块冲到圆轨道最高点时压力传感器2显示示数为F2=1.5N,由以上数据回答下面的问题.(不计空气阻力,取g=10m/s2)