题目内容
4.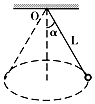 长为L的轻质细线,拴一质量为m的小球,一端固定于O点,让小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,已知摆线与竖直方向的夹角是α,求:
长为L的轻质细线,拴一质量为m的小球,一端固定于O点,让小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,已知摆线与竖直方向的夹角是α,求:(1)细线的拉力F;
(2)小球运动的线速度的大小.
分析 (1)对小球受力分析,根据平行四边形定则求出细线的拉力大小.
(2)根据合力提供向心力,结合牛顿第二定律求出线速度的大小.
解答 解: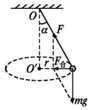 (1)对小球受力分析如图所示,小球受重力mg和绳子的拉力F.因为小球在水平面内做匀速圆周运动,所以小球受到的合力指向圆心O',且沿水平方向.由平行四边形定则得小球受到的合力大小为:F合=mgtanα,
(1)对小球受力分析如图所示,小球受重力mg和绳子的拉力F.因为小球在水平面内做匀速圆周运动,所以小球受到的合力指向圆心O',且沿水平方向.由平行四边形定则得小球受到的合力大小为:F合=mgtanα,
细线对小球的拉力大小为:F=$\frac{mg}{cosα}$.
(2)由牛顿第二定律得:mgtanα=m$\frac{{v}^{2}}{r}$,
由几何关系得:r=Lsinα,
代入数据解得小球做匀速圆周运动的线速度的大小为:v=$\sqrt{gLsinαtanα}$.
答:(1)细线的拉力F为$\frac{mg}{cosα}$;
(2)小球运动的线速度的大小为$\sqrt{gLsinαtanα}$.
点评 解决本题的关键能够正确地受力分析,结合牛顿第二定律进行求解,知道小球做圆周运动向心力的来源.

练习册系列答案
相关题目
14.有一个向西做匀速直线运动的质点,某时刻突然开始受到一个向南的恒力,则( )
| A. | 该质点立刻向南做直线运动 | |
| B. | 该质点做曲线运动 | |
| C. | 该质点先做曲线运动,后向南做直线运动 | |
| D. | 该质点的合速度方向最终会指向南方 |
15.与门电路的逻辑关系可表示为Z=A×B,下列结果错误的是 ( )
| A. | 0×0=0 | B. | 0×1=0 | C. | 1×0=1 | D. | 1×1=1 |
12.下列说法正确的是( )
| A. | 一切机械波和光的传播都需要介质 | |
| B. | 两列波在介质中叠加,一定能产生干涉现象 | |
| C. | “闻其声而不见其人”是声波的衍射现象 | |
| D. | “多普勒效应”是由于观察者和波源的相对运动使波源的频率发生变化而产生的 |
6.“套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.3m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为1m.假设直杆与环的中心位于同一竖直平面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,重力加速度g=10m/s2.则( )
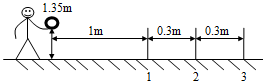

| A. | 如果能够套中直杆,环抛出时的水平初速度不能小于1.9m/s | |
| B. | 如果能够套中第2根直杆,环抛出时的水平初速度范围在2.4m/s到2.8m/s之间 | |
| C. | 如果以2m/s的水平初速度将环抛出,就可以套中第1根直杆 | |
| D. | 如果环抛出的水平速度大于3.3m/s,就不能套中第3根直杆 |
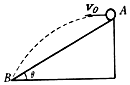 如图所示,斜面高lm,倾角θ=30°,在斜面的顶点A以速度v0水平抛出一小球,小球刚好落于斜面底部B点,不计空气阻力,g取10m/s2,求小球在空中运动的时间t和小球抛出的速度v0.(计算结果可保留根号)
如图所示,斜面高lm,倾角θ=30°,在斜面的顶点A以速度v0水平抛出一小球,小球刚好落于斜面底部B点,不计空气阻力,g取10m/s2,求小球在空中运动的时间t和小球抛出的速度v0.(计算结果可保留根号)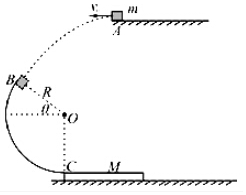 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点,C点右侧的光滑水平面上紧挨C点静止放置一木板.木板质量M=1kg,上表面与C点等高.质量为m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ=0.2,取g=10m/s2.求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点,C点右侧的光滑水平面上紧挨C点静止放置一木板.木板质量M=1kg,上表面与C点等高.质量为m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ=0.2,取g=10m/s2.求: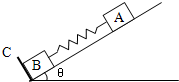 如图,在倾角为θ的光滑斜面上,有两个用轻质弹簧相连接的物体A、B.它们的质量均为m,弹簧的劲度系数k,C为一固定挡板.系统处一静止状态.现给A一个沿斜面向上的初速度v0,使A开始向上运动,当B刚要离开C时,A的速度多大?
如图,在倾角为θ的光滑斜面上,有两个用轻质弹簧相连接的物体A、B.它们的质量均为m,弹簧的劲度系数k,C为一固定挡板.系统处一静止状态.现给A一个沿斜面向上的初速度v0,使A开始向上运动,当B刚要离开C时,A的速度多大?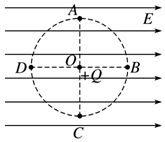 如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正点电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则A点的场强大小为$\sqrt{{E}^{2}+{k}^{2}\frac{{Q}^{2}}{{r}^{4}}}$.
如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正点电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则A点的场强大小为$\sqrt{{E}^{2}+{k}^{2}\frac{{Q}^{2}}{{r}^{4}}}$.