��Ŀ����
16�� ��ͼ��ʾ��������Ȧabcd������ΪN=50�ѣ���Ȧab�ı߳�ΪL1=0.2m��bc�ı߳�ΪL2=0.25m���ڴŸ�Ӧǿ��ΪB=0.4T����ǿ�ų��У��ƴ�ֱ�ڴŸ�����ͨ����Ȧ���ߵ�OO��������ת����ת���Ľ��ٶȦ�=10��rad/s������
��ͼ��ʾ��������Ȧabcd������ΪN=50�ѣ���Ȧab�ı߳�ΪL1=0.2m��bc�ı߳�ΪL2=0.25m���ڴŸ�Ӧǿ��ΪB=0.4T����ǿ�ų��У��ƴ�ֱ�ڴŸ�����ͨ����Ȧ���ߵ�OO��������ת����ת���Ľ��ٶȦ�=10��rad/s��������1��������Ȧƽ�������ͨ����m��
��2������Ȧ�в���������Ӧ�綯�ƴ�С��
��3������Ȧ��ͼʾλ�ÿ�ʼ��ת��90�������ƽ����Ӧ�綯�ƵĴ�С��
���� ��1���ɴ�ͨ���Ķ����������ͨ����
��2��ÿ���߿�ͨ��������ʱ����������ı䣻����ͨ��Ϊ��ʱ���߿��и��ٶ�������ĵ綯��Ҳ���
��3�����ݷ����ڵ�Ÿ�Ӧ�������ƽ���綯�ƣ�
��� �⣺��1��������Ȧƽ�������ͨ�� ��m=BS=Bl1l2=0.4��0.2��0.25=0.02Wb
��2����Ȧ��ͼʾλ��ʱ�綯�ƴﵽ���ֵ����ʱ��Ӧ�綯�Ƶ�ֵΪ
e=Em=NBS��=NBl1l2��=50��0.4��0.2��0.25��10��=314 V
��3����Ȧת��һȦ��ʱ$T=\frac{2��}{��}=\frac{2��}{10��}=0.2s$
����Ȧ��ͼʾλ�ÿ�ʼ��ת��900��ʱ $��t=\frac{1}{4}T=0.05s$
��ô��Ȧ�в�����ƽ����Ӧ�綯��Ϊ$E=n\frac{����}{��t}=\frac{50��0.02}{0.05}=20$V
�𣺣�1��������Ȧƽ�������ͨ����mΪ0.02Wb��
��2����Ȧ�в���������Ӧ�綯�ƴ�СΪ314V��
��3������Ȧ��ͼʾλ�ÿ�ʼ��ת��90�������ƽ����Ӧ�綯�ƵĴ�СΪ20V��
���� �߿�����ǿ�ų�������ת������������ʽ��������������ڵ����������������������ɽ�������Чֵ��ȷ�������漰����ѹֵʱ���������ֵ��ȷ������ͨ��ijһ����ʱ������ƽ��ֵ����

| A�� | 1.502m | B�� | 1.6214m | C�� | 12.4cm | D�� | 4.30mm |
 ��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���O������Բ���˶�����֪A��B������A��O����ļн����Ϊ�ȣ�������A��B�Ľ��ٶ�֮��$\frac{{��}_{1}}{{��}_{2}}$���ڣ�������
��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���O������Բ���˶�����֪A��B������A��O����ļн����Ϊ�ȣ�������A��B�Ľ��ٶ�֮��$\frac{{��}_{1}}{{��}_{2}}$���ڣ�������| A�� | sin3�� | B�� | $\frac{1}{si{n}^{3}��}$ | C�� | $\sqrt{si{n}^{3}��}$ | D�� | $\sqrt{\frac{1}{si{n}^{3}��}}$ |
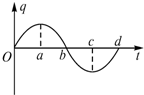
| A�� | ��b��dʱ�̣���·�е�����С | B�� | ��a��bʱ���ڣ��糡��ת��Ϊ�ų��� | ||
| C�� | a��cʱ�̣��糡����Ϊ�� | D�� | ��O��a��c��dʱ���ڣ������������ |
 ��ͼ��ʾ��ͼa��b��c��Բ�ľ��ڵ������ת�����ϣ��Ի��Ƶ���������Բ���˶����ԣ�������
��ͼ��ʾ��ͼa��b��c��Բ�ľ��ڵ������ת�����ϣ��Ի��Ƶ���������Բ���˶����ԣ�������| A�� | ���ǵĹ������Ϊa | B�� | ���ǵĹ������Ϊb | ||
| C�� | ���ǵĹ������Ϊc | D�� | ͬ�����ǵĹ��ֻ����Ϊb |
 ��һ��Բ������ש���������ͼ��ʾ���뾶ΪR��OΪԲ�ģ�һ��ƽ�й������AC�����䣬O�����ǡ��������ߣ���֪����ש��������Ϊ$\sqrt{2}$������OB�γ�������Ŀ��ȣ�
��һ��Բ������ש���������ͼ��ʾ���뾶ΪR��OΪԲ�ģ�һ��ƽ�й������AC�����䣬O�����ǡ��������ߣ���֪����ש��������Ϊ$\sqrt{2}$������OB�γ�������Ŀ��ȣ�
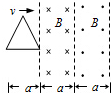 ��ͼ��ʾ��һ�߳�Ϊa������ΪR�ĵȱ��������߿����������������ٶ�v���ٴ������Ⱦ�Ϊa��������ǿ�ų��������ų��Ÿ�Ӧǿ�ȵĴ�С��ΪB�������෴���߿��˶�������ױ�ƽ������ų���Ե��ֱ������ʱ�뷽��Ϊ����������ͼʾλ�ÿ�ʼ�߿��и�Ӧ����I�����˶������λ��x�Ĺ�ϵͼ��Ϊ��������
��ͼ��ʾ��һ�߳�Ϊa������ΪR�ĵȱ��������߿����������������ٶ�v���ٴ������Ⱦ�Ϊa��������ǿ�ų��������ų��Ÿ�Ӧǿ�ȵĴ�С��ΪB�������෴���߿��˶�������ױ�ƽ������ų���Ե��ֱ������ʱ�뷽��Ϊ����������ͼʾλ�ÿ�ʼ�߿��и�Ӧ����I�����˶������λ��x�Ĺ�ϵͼ��Ϊ��������



 ��ͼ��ʾ����ֱ������ϵxoy�ĵ�һ���������У�����y�����������ǿ�糡����ǿ�Ĵ�СΪE=kv0���ڵڶ�������һ�뾶Ϊr=L��Բ���������ǿ�ų���Բ�δų���Բ��O����Ϊ ��-L��L������������ֱ�������P���N�㣬�ų�����ֱֽ�������x=3L����ֱ��x�����һƽ��ӫ��������x�ύ��ΪQ�������ĵ�������ͬ������v0��ֽ���ڴ�P�����Բ�δų������ӵ��ٶȷ�������x��������ɦȽǵķ�Χ�ڣ�������y��������ĵ��Ӿ����ų�����N�㣬�ٶ���x��������ɦȽǵĵ��Ӿ����ų�����M�㣬��M������Ϊ��0��1.5L�������Ե��Ӽ��������������Ƶ��ӵ����������ӵıȺ�Ϊ$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$����
��ͼ��ʾ����ֱ������ϵxoy�ĵ�һ���������У�����y�����������ǿ�糡����ǿ�Ĵ�СΪE=kv0���ڵڶ�������һ�뾶Ϊr=L��Բ���������ǿ�ų���Բ�δų���Բ��O����Ϊ ��-L��L������������ֱ�������P���N�㣬�ų�����ֱֽ�������x=3L����ֱ��x�����һƽ��ӫ��������x�ύ��ΪQ�������ĵ�������ͬ������v0��ֽ���ڴ�P�����Բ�δų������ӵ��ٶȷ�������x��������ɦȽǵķ�Χ�ڣ�������y��������ĵ��Ӿ����ų�����N�㣬�ٶ���x��������ɦȽǵĵ��Ӿ����ų�����M�㣬��M������Ϊ��0��1.5L�������Ե��Ӽ��������������Ƶ��ӵ����������ӵıȺ�Ϊ$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$����