题目内容
7. 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
分析 根据题意知道当行星处于最大视角处时,地球和行星的连线应与行星轨道相切,运用几何关系求解问题.
解答 解:人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,如图:
根据几何关系有RB=RAsinθ
根据开普勒第三定律有:$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$
所以:$\frac{ω_1}{ω_2}$=$\frac{{T}_{B}}{{T}_{A}}$=$\sqrt{\frac{{R}_{B}^{3}}{{R}_{A}^{3}}}$=$\sqrt{{sin}^{3}θ}$
故选:C.
点评 能根据题目给出的信息分析视角最大时的半径特征,在圆周运动中涉及几何关系求半径是一个基本功问题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
9.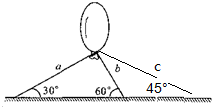 如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )
如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )
 如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )
如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )| A. | 细线受到的拉力中Ta一定最大 | |
| B. | 三根细线的拉力都不为零时,有可能Ta=Tb=Tc | |
| C. | 三根细线的拉力的竖直分量之和一定等于F | |
| D. | 三根细线的拉力的竖直分量之和一定小于F |
18. 如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
 如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )| A. | 电容器两极板间电压值变大 | B. | 电荷的电势能变大 | ||
| C. | 负电荷所在处的电势升高 | D. | 电容器两极板间的电场强度变小 |
15.对于相互接触的两个物体之间,同一接触面上的弹力和摩擦力,以下说法中正确的是( )
| A. | 有弹力必有摩擦力 | B. | 有摩擦力必有弹力 | ||
| C. | 摩擦力的大小一定与弹力成正比 | D. | 摩擦力的方向一定与运动方向相反 |
2.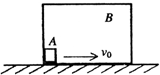 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )| A. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{6μg}$ | B. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{5μg}$ | ||
| C. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{7μg}$ | D. | t=$\frac{{5(\sqrt{v_0^2-2μgL}-\sqrt{2μgS})}}{7μg}$ |
12.据每日邮报2014年4月18日报道,美国国家航空航天局(NASA)目前宣布首次在太阳系外发现“类地”行星Kepler-186f.假如宇航员乘坐宇宙飞船到达该行星,进行科学观测:该行星自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t1;宇航员在该行星“赤道”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t2.则行星的半径R的值( )
| A. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| B. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| C. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| D. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ |
17.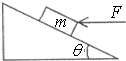 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )| A. | 力F所做的功FSsinθ | |
| B. | 斜面体对物体做的功为mgSsinθ-FScosθ | |
| C. | 物体摩擦力所做的功为μ(mgcosθ-Fsinθ)S | |
| D. | 物体的重力做功为mgS |
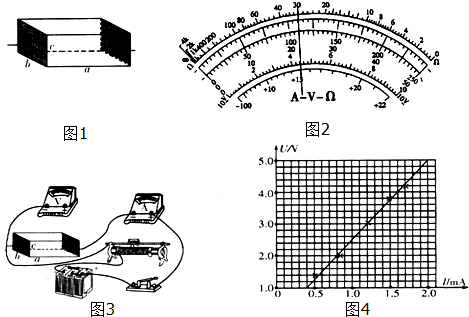
 如图所示,矩形线圈abcd的匝数为N=50匝,线圈ab的边长为L1=0.2m,bc的边长为L2=0.25m,在磁感应强度为B=0.4T的匀强磁场中,绕垂直于磁感线且通过线圈中线的OO′轴匀速转动,转动的角速度ω=10πrad/s,试求:
如图所示,矩形线圈abcd的匝数为N=50匝,线圈ab的边长为L1=0.2m,bc的边长为L2=0.25m,在磁感应强度为B=0.4T的匀强磁场中,绕垂直于磁感线且通过线圈中线的OO′轴匀速转动,转动的角速度ω=10πrad/s,试求: