题目内容
5. 如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求:
如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求:(1)圆形磁场的磁感应强度大小;
(2)θ角的大小;
(3)电子打到荧光屏上距Q点的最远距离.
分析 (1)速度沿y轴正方向的电子经过N点,结合几何关系求解轨道半径;根据牛顿第二定律列式求解磁感应强度;
(2)画出速度与x轴正方向成θ角的电子经过磁场过程的轨迹,结合几何关系确定轨道对应的圆心角;
(3)所有的电子以平行于x轴正方向的速度进入电场中做类似平抛运动,根据类似平抛运动的分运动公式列式求解即可.
解答 解:(1)由于速度沿y轴正方向的电子经过N点,因而电子在磁场中做圆周运动的半径为:
R=L
而 $q{v}_{0}B=\frac{m{v}_{0}^{2}}{R}$
联立解得 B=K
(2)电子在磁场中做圆周运动的圆心为O′,电子离开磁场时的位置为P′,连接POP′O′可知该四边形为菱形,由于PO竖直,因而半径P′O′也为竖直方向,电子离开磁场时速度一定沿x轴正方向.
由图可知 Lsin(θ-90°)+L=1.5L
解得:θ=120°
(3)由(2)可知,所有的电子以平行于x轴正方向的速度进入电场中做类似平抛运动,设电子在电场的运动时间为t,竖直方向位移为y,水平位移为x,则
水平方向:x=v0t
竖直方向:$y=\frac{1}{2}a{t}^{2}$
eE=ma
vy=at
联立解得:x=$\sqrt{2Ly}$
设电子最终打在光屏的最远点距Q点为H,电子射出电场时的夹角为θ,有:
$tanθ=\frac{{v}_{y}}{{v}_{x}}=\sqrt{\frac{2y}{L}}$
有:H=(3L-x)tanθ=$(3\sqrt{L}-\sqrt{2y})•\sqrt{2y}$
当$(3\sqrt{L}-\sqrt{2y})=\sqrt{2y}$时,即$y=\frac{9}{8}L$时,H有最大值.
由于$\frac{9}{8}L<1.5$L 所以 ${H}_{max}=\frac{9}{4}L$
答:(1)圆形磁场的磁感应强度大小是K;
(2)θ角的大小是120°;
(3)电子打到荧光屏上距Q点的最远距离是$\frac{9}{4}L$.
点评 本题关键是明确粒子的受力情况和运动规律,画出临界轨迹,结合牛顿第二定律、类似平抛运动的分运动规律和几何关系分析.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案| A. | 有弹力必有摩擦力 | B. | 有摩擦力必有弹力 | ||
| C. | 摩擦力的大小一定与弹力成正比 | D. | 摩擦力的方向一定与运动方向相反 |
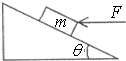 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )| A. | 力F所做的功FSsinθ | |
| B. | 斜面体对物体做的功为mgSsinθ-FScosθ | |
| C. | 物体摩擦力所做的功为μ(mgcosθ-Fsinθ)S | |
| D. | 物体的重力做功为mgS |
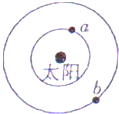
| A. | 行星a的线速度较小 | B. | 行星a的角速度较小 | ||
| C. | 行星a的周期较短 | D. | 行星a的向心加速度较小 |
 2012年4月16日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每378天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )
2012年4月16日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每378天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )| A. | 土星公转的速率比地球大 | |
| B. | 土星公转的向心加速度比地球小 | |
| C. | 土星公转的周期大于地球的公转周期 | |
| D. | 假如土星适度加速,有可能与地球实现对接 |
 如图所示,矩形线圈abcd的匝数为N=50匝,线圈ab的边长为L1=0.2m,bc的边长为L2=0.25m,在磁感应强度为B=0.4T的匀强磁场中,绕垂直于磁感线且通过线圈中线的OO′轴匀速转动,转动的角速度ω=10πrad/s,试求:
如图所示,矩形线圈abcd的匝数为N=50匝,线圈ab的边长为L1=0.2m,bc的边长为L2=0.25m,在磁感应强度为B=0.4T的匀强磁场中,绕垂直于磁感线且通过线圈中线的OO′轴匀速转动,转动的角速度ω=10πrad/s,试求: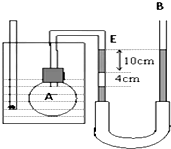 如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时:
如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时:
 如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求:
如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求: