��Ŀ����
1������ͼ1��ʾ��ʵ��װ��̽������Ķ��ܱ仯�����������Ĺ�ϵʱ��ʵ�����õĵ�ԴΪѧ����Դ�������ѹ�н������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬����ʱ�����ش����ŵ�ֽ���ϴ��һϵ�еĵ㣬��ͼ��ֽ���ϵĵ㼣���в���������֪������Ķ��� �仯�����������Ĺ�ϵ��
��1�����������������
A������ͼʾ����װ��ʵ��װ�ã�
B��������ʱ���ӵ�4��6V�ġ�����������ϣ�
C������ƽ����ش���������
D�����ͷ��ش������ͨ��Դ��ֽ�������ش��˶�������ʱ����ֽ���ϴ���һϵ�еĵ㣻
E������ֽ����ijЩ���ľ��룻
F�����ݲ����Ľ�������ش���������ж��ܵı仯�Ƿ�����������Ĺ���
����������û�б�Ҫ����C�������������D��������Ӧ����ĸ��
��2��ʹ������Ϊm���ش��ʹ���ʱ��̽������Ķ��ܱ仯�����������Ĺ�ϵʵ���У���ѡ����ֽ��������ȡ��������ͼ2��ʾ��ֽ��������ĵ��¼�������ڲ�ͬʱ�̵�λ�ã���ôֽ����������ҡ�������������������������֮���ʱ������ΪT����OΪ���µĵ�һ���㣮������ʱ����㡰3��ʱ������Ķ��ܱ���ʽΪEk3=m$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$������������˶����OΪ�ο��㣬����ڡ�3����Ĺ����У���������ɵķ�Χ�ڣ�������֤ʵ����۵ı���ʽ��$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$=gs3��
���� ��1��ͨ��ʵ���ԭ��ȷ����Ҫ���������������Ӷ�ȷ������Ҫ�IJ������裮ʵ��ʱ������ʱ��Ӧ�ӽ�����Դ���Ƚ�ͨ��Դ�����ͷ�ֽ����
��2��ֽ��ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȣ��Ӷ�������ܣ����ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
��� �⣺��1����Ϊ�����DZȽ�mgh��$\frac{1}{2}$mv2�Ĵ�С��ϵ����m��Լȥ�Ƚϣ�����Ҫ����ƽ����Cû�б�Ҫ��
��ʼ��¼ʱ��Ӧ�ȸ�����ʱ��ͨ���㣬Ȼ�����ͷ��ش�����������ֽ��һͬ���£�����ȷſ�ֽ�����������䣬�ٽ�ͨ����ʱʱ���ĵ�Դ�����������˶��Ͽ죬���������ݵIJɼ��ʹ��������ʵ������ϴ�����ʲ���D����
��2��ʵ�����ش��ǴӾ�ֹ�ͷŵģ��ٶ����������ش�������ֽ���ٶȽ�С������������ͼ�п��Կ���Ӧ�������������������
�����ȱ���ֱ���˶�������
v3=$\frac{{x}_{24}}{2T}$=$\frac{{s}_{4}-{s}_{2}}{2T}$
Ek3=$\frac{1}{2}$mv32=m$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$
��������˶����OΪ�ο���
3����������ܵ���Ep=-mgh=-mgs3 ��
����ڵ㡰3��ʱ����Ļ�е�ܱ���ʽΪ��m$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$=mgs3
��$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$=gs3��
�ʴ�Ϊ����1��C��D����2����Ek3=m$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$��$\frac{��{s}_{4}-{s}_{2}��^{2}}{8{T}^{2}}$=gs3
���� Ҫ�����˶�ѧ�Ĺ�ʽȥ����ٶȴ�С����������ܣ�ij��λ�õ��������ܵ����Ҫ�涨�������森ֻ����ȷ��ʵ��ԭ���Լ�ʵ������ݲ�����������ȷ����ʵ������ľ��庬�壬���Ҫ��ƽʱѵ���м�ǿ��ϰ��

 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�| A�� | ����ѧ�ҵڹ����̫��ϵ�����˶������� | |
| B�� | ����ѧ��ţ������������������ɲ���������������������ֵ | |
| C�� | ���ĵ�����ʵ��ķ������������������G | |
| D�� | �ǵ�˹����άҮ���Զ������������������ɼ�����������ǵĹ���������dz���Ϊ���ʼ��·��ֵ����ǡ� |
| A�� | R=$\frac{��{{t}_{2}}^{2}+{{t}_{1}}^{2}��h{T}^{2}}{4{��}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| B�� | R=$\frac{��{{t}_{2}}^{2}+{{t}_{1}}^{2}��h{T}^{2}}{2{��}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| C�� | R=$\frac{��{{t}_{2}}^{2}-{{t}_{1}}^{2}��h{T}^{2}}{2{��}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| D�� | R=$\frac{��{{t}_{2}}^{2}-{{t}_{1}}^{2}��h{T}^{2}}{4{��}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ |
| A�� | ¬ɪ��ͨ��������ɢ��ʵ�������ԭ�Ӻ�ʽ�ṹ��ģ�� | |
| B�� | ���˹Τ���ȴ�ʵ����֤ʵ�˵�Ų��Ĵ��� | |
| C�� | ����˹̹��������ӡ����ۣ��ɹ��ضԹ��ЧӦ�����˽��� | |
| D�� | ��������У��˶��е�ʱ�ӻ�Ⱦ�ֹʱ�ߵÿ� |
 ��ͼ��ʾ��������Ȧabcd������ΪN=50�ѣ���Ȧab�ı߳�ΪL1=0.2m��bc�ı߳�ΪL2=0.25m���ڴŸ�Ӧǿ��ΪB=0.4T����ǿ�ų��У��ƴ�ֱ�ڴŸ�����ͨ����Ȧ���ߵ�OO��������ת����ת���Ľ��ٶȦ�=10��rad/s������
��ͼ��ʾ��������Ȧabcd������ΪN=50�ѣ���Ȧab�ı߳�ΪL1=0.2m��bc�ı߳�ΪL2=0.25m���ڴŸ�Ӧǿ��ΪB=0.4T����ǿ�ų��У��ƴ�ֱ�ڴŸ�����ͨ����Ȧ���ߵ�OO��������ת����ת���Ľ��ٶȦ�=10��rad/s������ �ڡ��о�ƽ�������˶�����ʵ���У�
�ڡ��о�ƽ�������˶�����ʵ���У�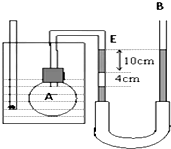 ��ͼ��ʾΪ��֤�������ɵ�ʵ��װ�ã�AΪ��ƿ������������BΪU�ιܣ��²���ϳ�������������������װ������U�ι����10cmˮ�������·�����һ�γ�Ϊ4cm�Ŀ����������ˮ�����ϱ������־��E���룮��ʼʱ��ƿ����ˮ����ˮ��Ϊ7�棬U�ι�����ˮ������ƽ����ˮ������63��ʱ�������ұ߿���ˮ���ܵĸ߶ȣ�ʹ���ˮ�����ϱ��������־��E���룮��֪����ѹp0=76cmHg����ʱ��
��ͼ��ʾΪ��֤�������ɵ�ʵ��װ�ã�AΪ��ƿ������������BΪU�ιܣ��²���ϳ�������������������װ������U�ι����10cmˮ�������·�����һ�γ�Ϊ4cm�Ŀ����������ˮ�����ϱ������־��E���룮��ʼʱ��ƿ����ˮ����ˮ��Ϊ7�棬U�ι�����ˮ������ƽ����ˮ������63��ʱ�������ұ߿���ˮ���ܵĸ߶ȣ�ʹ���ˮ�����ϱ��������־��E���룮��֪����ѹp0=76cmHg����ʱ�� ��ͼ��ʾ���ڹ⻬��ˮƽ���ϣ���A��B��C�������壬C������뵯�����������ɴ���ԭ������֪A B C���������������Ϊ4kg����������B��C���ھ�ֹ״̬��A��V0=6m/s���ٶ������˶���������B��ײ��ճ��һ����������˶�����
��ͼ��ʾ���ڹ⻬��ˮƽ���ϣ���A��B��C�������壬C������뵯�����������ɴ���ԭ������֪A B C���������������Ϊ4kg����������B��C���ھ�ֹ״̬��A��V0=6m/s���ٶ������˶���������B��ײ��ճ��һ����������˶�����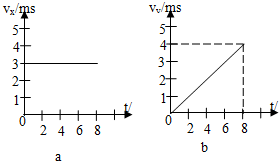 ��ͼ��ʾ����ͼ��ʾij������x�᷽���Ϸ��ٶȵ�v-tͼ��bͼ��ʾ��������y���Ϸ��ٶ�ͼ��
��ͼ��ʾ����ͼ��ʾij������x�᷽���Ϸ��ٶȵ�v-tͼ��bͼ��ʾ��������y���Ϸ��ٶ�ͼ��