题目内容
18.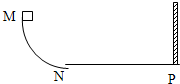 如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求:
如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求:(1)木块第一次过N点时对N点的压力
(2)木块与竖直挡板碰撞前瞬时的速度
(3)物块停止的位置与N点距离.
分析 (1)第一次从静止开始下滑到N点过程中机械能守恒,求出到达N的速度,由重力和N点对木块的支持力的合力充当向心力求出木块第一次过N点时对N点的压力.
(2)在NP段由摩擦力做负功使木块的动能减小,由动能定理求出木板与竖直挡板碰撞前瞬时速度.
(3)对物体运动过程进行分析,选择某一过程利用功能关系进行研究,能列出等式求未知量.
解答 解:(1)设物体过N点时的速度为vN,木块第一次过N点时对N点的压力大小为FN
则由机械能守恒得:mgh=$\frac{1}{2}m{{v}_{N}}^{2}$
到达N点时,由圆周运动得:$\frac{m{{v}_{N}}^{2}}{h}$=FN-mg
联立以上两式得:${v}_{N}=\sqrt{2gh}$,FN=3mg
(2)木块在NP段运动时所受摩擦力:f=μmg
设木块与竖直挡板碰撞前瞬时的速度为vP
由动能定理:$\frac{1}{2}m{{v}_{P}}^{2}=\frac{1}{2}m{{v}_{N}}^{2}-μmgs$
解得:vP=$\sqrt{2gh-2μgs}$
(3)根据功能原理,在物块从开始下滑到停止在水平轨道上的过程中,物块的重力势能的减少△EP与物块克服摩擦力所做功的数值相等.
△EP=Wf-----①
设物块的质量为m,在水平轨道上滑行的总路程为s′,
则△EP=mgh-----②,
Wf=μmgs′--------③
连立①②③化简得:s′=$\frac{h}{μ}$
第一种可能是:物块与弹性挡板碰撞后,在到达N前停止,
则物块停止的位置距N的距离为:d=2s-s′=2s-$\frac{h}{μ}$
第二种可能是:物块与弹性挡板碰撞后,可再一次滑上光滑圆弧轨道,滑下后在水平轨道上停止,
则物块停止的位置距N的距离为:d1=s′-2s=$\frac{h}{μ}-2s$
答:(1)木块第一次过N点时对N点的压力为3mg;
(2)木块与竖直挡板碰撞前瞬时的速度为$\sqrt{2gh-2μgs}$;
(3)物块停止的位置与N点距离可能为(2s-$\frac{h}{μ}$)或者($\frac{h}{μ}-2s$).
点评 根据题意要能考虑到物体运动可能经历的过程,利用功能关系得出水平轨道上滑行的总路程.

 快捷英语周周练系列答案
快捷英语周周练系列答案 如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中( )
如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中( )| A. | 物块a的重力势能减少mgh | |
| B. | 摩擦力对a做的功等于a机械能的增量 | |
| C. | 摩擦力对a做的功等于物块a、b动能增量之和 | |
| D. | 任意时刻,重力对a、b做功的瞬时功率大小相等 |

| A. | 穿过回路abPMa的磁通量均匀增加 | |
| B. | 棒由静止向上做匀加速运动 | |
| C. | 拉力F做的功等于回路产生的热量与金属棒ab增加的重力势能之和 | |
| D. | 拉力F做的功与安倍力做的功之和等于金属棒ab增加的机械能 |
 如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,恰好落至斜面底端,不计小球运动过程中所受的空气阻力,设重力加速度为g,则小球从抛出到离斜面距离最大所经历的时间为( )
如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,恰好落至斜面底端,不计小球运动过程中所受的空气阻力,设重力加速度为g,则小球从抛出到离斜面距离最大所经历的时间为( )| A. | $\sqrt{\frac{h}{2g}}$ | B. | $\sqrt{\frac{hsinα}{2g}}$ | C. | $\sqrt{\frac{2h}{g}}$ | D. | $\sqrt{\frac{h}{g}}$ |
| A. | 物体运动的加速度等于0,则速度一定等于0 | |
| B. | 物体的速度变化越快,加速度越大 | |
| C. | 物体具有向东的加速度,其速度的方向一定向东 | |
| D. | 物体做直线运动,加速度变小,则速度一定变小 |
 如图所示,物体静止于倾斜放置的木板上,当倾角θ由很小缓慢增大到90°的过程中,木板对物体的支持力FN和摩擦力f的变化情况是( )
如图所示,物体静止于倾斜放置的木板上,当倾角θ由很小缓慢增大到90°的过程中,木板对物体的支持力FN和摩擦力f的变化情况是( )| A. | FN、f都增大 | B. | FN、f都减少 | ||
| C. | FN增大,f先减小后增大 | D. | FN减小,f先增大后减小 |
 如图所示电路中,电源电动势为E,内阻为r,R1,R2为定值电阻,R3为可变电阻,C为电容器.在可变电阻R3的阻值由较大慢慢变小的过程中( )
如图所示电路中,电源电动势为E,内阻为r,R1,R2为定值电阻,R3为可变电阻,C为电容器.在可变电阻R3的阻值由较大慢慢变小的过程中( )| A. | 流过的电流方向是由下向上 | B. | 电容器板间场强逐渐变大 | ||
| C. | 电容器的电容逐渐减小 | D. | 电源内部消耗的功率变小 |
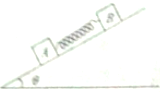 质量分别为mA和mB的物块A、B与斜面间的动摩擦因数分别为μA和μB,它们之间用轻质弹簧相连,且弹簧与斜面平行,两物块和弹簧沿倾角为θ的斜面以相同的加速度下滑,如图所示.重力加速度为g,则:
质量分别为mA和mB的物块A、B与斜面间的动摩擦因数分别为μA和μB,它们之间用轻质弹簧相连,且弹簧与斜面平行,两物块和弹簧沿倾角为θ的斜面以相同的加速度下滑,如图所示.重力加速度为g,则: 如图所示,M、N为两块水平放置的平行金属板,板长为L,板间距离也为L.两板间加有电压,且M板电势高于N板.今有-质量为m,带电量为-q的小球(可视为质点)沿平行于金属板的中央直线,以速度v水平飞入两板间
如图所示,M、N为两块水平放置的平行金属板,板长为L,板间距离也为L.两板间加有电压,且M板电势高于N板.今有-质量为m,带电量为-q的小球(可视为质点)沿平行于金属板的中央直线,以速度v水平飞入两板间