题目内容
9.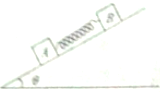 质量分别为mA和mB的物块A、B与斜面间的动摩擦因数分别为μA和μB,它们之间用轻质弹簧相连,且弹簧与斜面平行,两物块和弹簧沿倾角为θ的斜面以相同的加速度下滑,如图所示.重力加速度为g,则:
质量分别为mA和mB的物块A、B与斜面间的动摩擦因数分别为μA和μB,它们之间用轻质弹簧相连,且弹簧与斜面平行,两物块和弹簧沿倾角为θ的斜面以相同的加速度下滑,如图所示.重力加速度为g,则:(1)弹簧的弹力大小和方向如何?
(2)若把轻质弹簧换成细线,则细线的拉力大小和方向又如何?
分析 对整体分析,根据牛顿第二定律求出整体的加速度,隔离对A分析,结合牛顿第二定律求出弹簧的弹力和细线的拉力的大小和方向.
解答 解:(1)对整体分析,整体的加速度$a=\frac{({m}_{A}+{m}_{B})gsinθ-{μ}_{A}{m}_{A}gcosθ-{μ}_{B}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$=$gsinθ-\frac{{μ}_{A}{m}_{A}gcosθ+{μ}_{B}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
隔离对A分析,根据牛顿第二定律得,mAgsinθ-μAmAgcosθ-F=mAa,
解得F=$\frac{({μ}_{B}-{μ}_{A}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
若μB>μA,弹簧处于伸长状态,对A的弹力方向沿斜面向上,大小为F=$\frac{({μ}_{B}-{μ}_{A}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
若μB<μA,弹簧处于压缩状态,对A的弹力方向沿斜面向下,大小为$F=\frac{({μ}_{A}-{μ}_{B}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
(2)将轻质弹簧换成细线,若μB>μA,细线对A的拉力方向沿斜面向上,大小为F=$\frac{({μ}_{B}-{μ}_{A}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$.
若μB<μA,则细线的拉力为零.
答:(1)若μB>μA,弹簧处于伸长状态,对A的弹力方向沿斜面向上,大小为F=$\frac{({μ}_{B}-{μ}_{A}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
若μB<μA,弹簧处于压缩状态,对A的弹力方向沿斜面向下,大小为$F=\frac{({μ}_{A}-{μ}_{B}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$,
(2)若μB>μA,细线对A的拉力方向沿斜面向上,大小为F=$\frac{({μ}_{B}-{μ}_{A}){m}_{A}{m}_{B}gcosθ}{{m}_{A}+{m}_{B}}$.
若μB<μA,则细线的拉力为零.
点评 本题考查了牛顿第二定律的基本运用,掌握整体法和隔离法的灵活运用,本题计算量较大,计算时需细心.

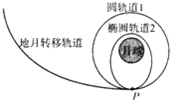 “嫦娥三号”登月探测器在月球成功着陆,标志着我国登月探测技术达到了世界领先水平.“嫦娥三号”绕月飞行的示意图如图所示,P点为变轨点,引力常量为G,则“嫦娥三号”( )
“嫦娥三号”登月探测器在月球成功着陆,标志着我国登月探测技术达到了世界领先水平.“嫦娥三号”绕月飞行的示意图如图所示,P点为变轨点,引力常量为G,则“嫦娥三号”( )| A. | 在轨道1上运行的周期小于在轨道2上运行的周期 | |
| B. | 沿两个不同轨道运行,经过P点时的线速度相同 | |
| C. | 沿两个不同的轨道运行,经过P点时所受月球引力相同 | |
| D. | 若已知轨道1上动行的周期和轨道半径,可求月球质量 |
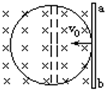 如图所示,粗细均匀的电阻为r的金属圆环,放在图示的匀强磁场中磁感应强度为B,圆环直径为d,长为L,电阻为$\frac{r}{2}$的金属棒ab放在圆环上,以速度v0向左运动,当ab棒运动到图示虚线位置时,金属棒两端电势差为( )
如图所示,粗细均匀的电阻为r的金属圆环,放在图示的匀强磁场中磁感应强度为B,圆环直径为d,长为L,电阻为$\frac{r}{2}$的金属棒ab放在圆环上,以速度v0向左运动,当ab棒运动到图示虚线位置时,金属棒两端电势差为( )| A. | 0 | B. | BLv | C. | $\frac{1}{2}$BLv | D. | $\frac{1}{3}$BLv |
| A. | 通过做大量实验后,胡克认为弹力一定与弹性形变量成正比 | |
| B. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| C. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| D. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 |
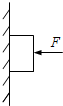
| A. | 木块重力与墙对木块的静摩擦力是一对平衡力 | |
| B. | 木块重力与墙对木块的静摩擦力是一对作用力与反作用力 | |
| C. | 木块对墙的压力与F是一对平衡力 | |
| D. | F与墙对木块的压力是一对作用力与反作用力 |
 如图是体育摄影中“追拍法”的成功之作,摄影师眼中清晰的滑板运动员是静止的,而模糊的背景是运动的,摄影师用自己的方式表达了运动的美.请问摄影师选择的参考系是( )
如图是体育摄影中“追拍法”的成功之作,摄影师眼中清晰的滑板运动员是静止的,而模糊的背景是运动的,摄影师用自己的方式表达了运动的美.请问摄影师选择的参考系是( )| A. | 滑板运动员 | B. | 步行的人 | C. | 大地 | D. | 太阳 |

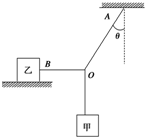 如图所示,质量为m1=5kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2=2kg的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin37°=0.6,cos37°=0.8,tan37°=0.75,g取10m/s2.设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1=5kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2=2kg的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin37°=0.6,cos37°=0.8,tan37°=0.75,g取10m/s2.设最大静摩擦力等于滑动摩擦力)求: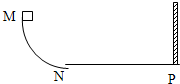 如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求:
如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求: