题目内容
13. 如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,恰好落至斜面底端,不计小球运动过程中所受的空气阻力,设重力加速度为g,则小球从抛出到离斜面距离最大所经历的时间为( )
如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,恰好落至斜面底端,不计小球运动过程中所受的空气阻力,设重力加速度为g,则小球从抛出到离斜面距离最大所经历的时间为( )| A. | $\sqrt{\frac{h}{2g}}$ | B. | $\sqrt{\frac{hsinα}{2g}}$ | C. | $\sqrt{\frac{2h}{g}}$ | D. | $\sqrt{\frac{h}{g}}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,当小球的速度方向与斜面平行时,距离斜面最远,结合平行四边形定则求出竖直分速度,根据速度时间公式求出运动的时间.
解答 解:根据h=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{2h}{g}}$,
则平抛运动的初速度为:${v}_{0}=\frac{hcotθ}{t}=\sqrt{\frac{gh}{2}}cotθ$,
当速度方向与斜面平行时,距离斜面最远,此时竖直分速度为:${v}_{y}={v}_{0}tanθ=\sqrt{\frac{gh}{2}}$,
则经历的时间为:t′=$\frac{{v}_{y}}{g}=\sqrt{\frac{h}{2g}}$,故A正确,B、C、D错误.
故选:A.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,知道当小球的速度方向与斜面平行时,距离斜面最远.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图所示,一质量为m的带电小球A用长度为l的绝缘丝质细线悬挂于天花板上的O点,在O点的正下方l处的绝缘支架上固定一个带与A同种电荷的小球B,两个带电小球都可视为点电荷.已知小球A静止时丝线OA与竖直方向的夹角为60°,设丝线中拉力为T,小球所受库仑力为F,下列关系式正确的是( )
如图所示,一质量为m的带电小球A用长度为l的绝缘丝质细线悬挂于天花板上的O点,在O点的正下方l处的绝缘支架上固定一个带与A同种电荷的小球B,两个带电小球都可视为点电荷.已知小球A静止时丝线OA与竖直方向的夹角为60°,设丝线中拉力为T,小球所受库仑力为F,下列关系式正确的是( )
 如图所示,一质量为m的带电小球A用长度为l的绝缘丝质细线悬挂于天花板上的O点,在O点的正下方l处的绝缘支架上固定一个带与A同种电荷的小球B,两个带电小球都可视为点电荷.已知小球A静止时丝线OA与竖直方向的夹角为60°,设丝线中拉力为T,小球所受库仑力为F,下列关系式正确的是( )
如图所示,一质量为m的带电小球A用长度为l的绝缘丝质细线悬挂于天花板上的O点,在O点的正下方l处的绝缘支架上固定一个带与A同种电荷的小球B,两个带电小球都可视为点电荷.已知小球A静止时丝线OA与竖直方向的夹角为60°,设丝线中拉力为T,小球所受库仑力为F,下列关系式正确的是( )| A. | T=$\frac{1}{2}$mg | B. | T=$\sqrt{3}$mg | C. | F=$\sqrt{3}$mg | D. | F=mg |
4.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所作科学贡献及物理思想方法的叙述中,正确的说法是( )
| A. | 通过做大量实验后,胡克认为弹力一定与弹性形变量成正比 | |
| B. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| C. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| D. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 |
8.下列关于惯性的说法中正确的是( )
| A. | 战斗机战斗前抛弃副油箱,是为了减小战斗机的惯性 | |
| B. | 火箭升空时,火箭的惯性随其速度的增大而增大 | |
| C. | 做自由落体运动的物体没有惯性 | |
| D. | 物体静止时的惯性比运动时大 |
5. 如图所示,叠放一起的a、b两物体在水平力F的作用下沿水平面作匀速直线运动,则关于b物体的受力情况说法正确的是( )
如图所示,叠放一起的a、b两物体在水平力F的作用下沿水平面作匀速直线运动,则关于b物体的受力情况说法正确的是( )
 如图所示,叠放一起的a、b两物体在水平力F的作用下沿水平面作匀速直线运动,则关于b物体的受力情况说法正确的是( )
如图所示,叠放一起的a、b两物体在水平力F的作用下沿水平面作匀速直线运动,则关于b物体的受力情况说法正确的是( )| A. | b物体可能受3个力作用 | B. | b物体可能受4个力作用 | ||
| C. | b物体可能受5个力作用 | D. | b物体可能受6个力作用 |
3.L是自感系数很大的线圈,但其自身的电阻几乎为零.A和B是两个相同的小灯泡.( )


| A. | 当开关由断开变为闭合时,A、B两灯均立即变亮且亮度不变 | |
| B. | 当开关由断开变为闭合时,A由亮变为更亮,B由亮变暗,直至不亮 | |
| C. | 当开关由闭合变为断开时,A、B均立即熄灭 | |
| D. | 当开关由闭合变为断开时,A立即熄灭,B亮一下熄灭 |
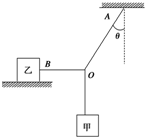 如图所示,质量为m1=5kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2=2kg的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin37°=0.6,cos37°=0.8,tan37°=0.75,g取10m/s2.设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1=5kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2=2kg的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin37°=0.6,cos37°=0.8,tan37°=0.75,g取10m/s2.设最大静摩擦力等于滑动摩擦力)求: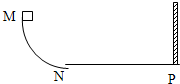 如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求:
如图,MNP为竖直面内一固定圆弧轨道,其$\frac{1}{4}$圆弧段MN与水平段NP相切与N,P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一质量为m的木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞(碰撞中无能量损失)后停止在水平轨道上某处.若在MN段的摩擦可以忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求: 如图所示,静止在水平桌面的纸带上有一质量为0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1.现用力向左以2m/s2的加速度将纸带从铁块下抽出.求:(不计铁块大小,铁块不滚动,g取10m/s2)
如图所示,静止在水平桌面的纸带上有一质量为0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1.现用力向左以2m/s2的加速度将纸带从铁块下抽出.求:(不计铁块大小,铁块不滚动,g取10m/s2)