题目内容
6.人类渴望探索宇宙,了解更多的地外文明,若假设某天人类发现了类地球行星,探测器飞近该星球后绕其环绕飞行,探测器记录了飞行的周期T和飞行的速度大小v以及飞行高度h,求:(1)该星球质量;
(2)该星球第一宇宙速度.
分析 (1)探测器绕星球做匀速圆周运动,根据万有引力等于向心力求出星球质量
(2)星球的第一宇宙速度即星球的近地卫星的运行速度
解答 解:(1)由$v=\frac{2πr}{T}$,得:$r=\frac{vT}{2π}$
根据万有引力提供向心力,有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$:
解得:$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}=\frac{4{π}_{\;}^{2}}{G{T}_{\;}^{2}}×\frac{{v}_{\;}^{3}{T}_{\;}^{3}}{(2π)_{\;}^{3}}$=$\frac{{v}_{\;}^{3}T}{2πG}$
(2)星球的半径为:$R=r-h=\frac{vT}{2π}-R$
根据万有引力提供向心力,有:$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{1}^{2}}{R}$
解得:${v}_{1}^{\;}=\sqrt{\frac{GM}{R}}=\sqrt{\frac{\frac{{v}_{\;}^{3}T}{2π}}{\frac{vT}{2π}-R}}$=$\sqrt{\frac{{v}_{\;}^{3}T}{vT-2πR}}$
答:(1)该星球质量$\frac{{v}_{\;}^{3}T}{2πG}$;
(2)该星球第一宇宙速度$\sqrt{\frac{{v}_{\;}^{3}T}{vT-2πR}}$
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
20.压敏电阻的阻值随所受压力的增大而减小,有位同学设计了利用压敏电阻判断升降机运动状态的装置,其工作原理如图1所示,将压敏电阻固定在升降机底板上,其上放置一个绝缘物块.0~t1时间内升降机停在某一楼层处,t1时刻升降机开始运动,从电流表中得到电流随时间变化的情况如图2所示,下列判断正确的是( )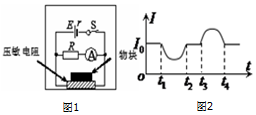

| A. | t1~t2时刻升降机一定在加速下降 | |
| B. | t1~t2时刻升降机一定在加速上升 | |
| C. | t2~t3时间内升降机一定处于匀速运动状态 | |
| D. | t2~t3时间内升降机可能处于静止状态 |
1.某个行星的质量是地球质量的一半,半径也是地球半径的一半.某运动员在地球上能举起250kg的杠铃,在该行星上最多能举起质量为多少的杠铃( )
| A. | 50kg | B. | 125kg | C. | 250kg | D. | 500kg |
18.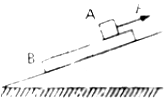 两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
 两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )
两个物块A、B叠放在光滑的斜面上,用方向与斜面平行的拉力F作用在A上,使两物块一起沿斜面向上做匀速运动,则下列说法中正确的有( )| A. | 物块B受到A的静摩擦力沿斜面向上 | B. | 物块B给A的静摩擦力沿斜面向上 | ||
| C. | 物块A所受到的静摩擦力大小等于F | D. | 物块A所受到的静摩擦力大小小于F |
15.一辆车以速度v行驶了一半的路程,接着以20km/h的速度跑完了余下的路程,若全程的平均速度是24km/h,则v是( )
| A. | 28 km/h | B. | 30km/h | C. | 22 km/h | D. | 44km/h |
16.轻质弹簧的原长为10cm,受到10N的压力作用时长度变为8cm,若此弹簧在20N拉力作用下长度变为(在弹性限度内)( )
| A. | 6cm | B. | 10cm | C. | 12cm | D. | 14cm |
 在电路图中,R1=2Ω,R2=4Ω,电压表示数为3V.求:
在电路图中,R1=2Ω,R2=4Ω,电压表示数为3V.求: 建筑工地上常用的一种“深穴打夯机”如图所示,电动机带动两个滚轮始终匀速转动.当夯杆在深穴底时,两个滚轮紧压夯杆,依靠摩擦力将夯杆提上来,在夯杆下端达到深穴口前,两个滚轮彼此分开,使夯杆下端与地面相平时,速度正好为零;然后,夯杆在自身重力的作用下落回深坑,夯实坑底;两个滚轮再次压紧,夯杆再次被提上来,如此循环运动.已知两个滚轮边缘的速度相同为v=3m/s,每个滚轮对夯杆的正压力N=3.25×104 N,滚轮和夯杆间的动摩擦因数μ=0.4,夯杆的质量m=2×103kg,坑深h=13.95m.假定在打夯的过程中坑的深度变化不大,可以视为不变.取g=10m/s2.求:
建筑工地上常用的一种“深穴打夯机”如图所示,电动机带动两个滚轮始终匀速转动.当夯杆在深穴底时,两个滚轮紧压夯杆,依靠摩擦力将夯杆提上来,在夯杆下端达到深穴口前,两个滚轮彼此分开,使夯杆下端与地面相平时,速度正好为零;然后,夯杆在自身重力的作用下落回深坑,夯实坑底;两个滚轮再次压紧,夯杆再次被提上来,如此循环运动.已知两个滚轮边缘的速度相同为v=3m/s,每个滚轮对夯杆的正压力N=3.25×104 N,滚轮和夯杆间的动摩擦因数μ=0.4,夯杆的质量m=2×103kg,坑深h=13.95m.假定在打夯的过程中坑的深度变化不大,可以视为不变.取g=10m/s2.求: