题目内容
10. 如图所示,光滑水平轨道左端与长L=1.25m的水平传送带AB相接,传送带逆时针匀速转动的速度υ0=1m/s.轻弹簧右端固定,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进人竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,长木板与水平地面间动摩擦因数μ3=0.026,g取10m/s2.求:
如图所示,光滑水平轨道左端与长L=1.25m的水平传送带AB相接,传送带逆时针匀速转动的速度υ0=1m/s.轻弹簧右端固定,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进人竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,长木板与水平地面间动摩擦因数μ3=0.026,g取10m/s2.求:(1)物块到达B点时速度υB的大小;
(2)弹簧被压缩时的弹性势能EP;
(3)小物块在长木板上滑行的最大距离s.
分析 (1)据恰好做圆周运动,利用牛顿运动定律列方程求解.(2)利用运动过程能量守恒即可求弹簧压缩时的弹性势能.(3)先据受力情况判断长木板的运动情况,再利用牛顿运动定律或动能定理求解.
解答 解:(1)物体恰好做圆周运动,在光滑半圆轨道最高点,据牛顿第二定律:mg=$\frac{m{v}_{B}^{2}}{R}$
解得:vB=$\sqrt{Rg}=\sqrt{10×0.4}m/s$=2m/s
(2)物体被弹簧弹出的过程中,物块和弹簧组成的系统机械能守恒:
Ep=$\frac{1}{2}m{v}_{A}^{2}$
由于vB>1m/s,所以物块在传送带上一直做匀减速运动
物块在传送带上据动能定理得:$-{f}_{1}L=\frac{1}{2}$$m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{A}^{2}$
又因为:f1=μ1mg
联立解得:Ep=1.2J
(3)物块从B到C过程中由机械能守恒定律得:mg•2R=$\frac{1}{2}m{v}_{C}^{2}-\frac{1}{2}m{v}_{B}^{2}$
解得:vC=$\sqrt{20}m/s$ ①
物块在长木板上滑行过程中,对长木板受力分析:
上表面受到的摩擦力f2=μ2mg=0.25N
下表面受到摩擦力:f3=μ3(M+m)g=0.26N>f2,所以长木板静止不动.
对物块在长木板上滑行过程由动能定理得:$-{f}_{2}s=0-\frac{1}{2}m{v}_{C}^{2}$ ②
联立①②解得:s=$\frac{m{v}_{C}^{2}}{2{f}_{2}}$=4m
答:1)物块到达B点时速度υB的大小2m/s;
(2)弹簧被压缩时的弹性势能1.2J;
(3)小物块在长木板上滑行的最大距离4m.
点评 分析透滑块的运动情况和受力情况是解题的关键,据受力情况判断滑块的运动是解题的核心,灵活利用牛顿运动定律、动能定理和能量守恒定律,基础题.

| A. | 地球同步卫星和地球同步,因此同步卫星的高度和线速度大小是一定的 | |
| B. | 地球同步卫星的角速度虽被确定,但高度和速度可以选择,高度增加,速度增大 | |
| C. | 地球同步卫星只能定点在赤道上空,相对地面静止不动 | |
| D. | 以上均不正确 |
 如图所示,一斜面体固定在一定高度的桌面的边缘,物块A和B用绕过斜面顶端定滑轮的轻绳连接,开始时,B处斜面底端且被固定,A紧靠着定滑轮用绳吊着,物块A的质量m1=2kg,物块B的质量m2=1.5kg,斜面的倾角θ=37°,斜面的长为2m,现由静止释放物块B,结果物块B在物块A的拉动下,经过3.16s运动到斜面顶端,求:
如图所示,一斜面体固定在一定高度的桌面的边缘,物块A和B用绕过斜面顶端定滑轮的轻绳连接,开始时,B处斜面底端且被固定,A紧靠着定滑轮用绳吊着,物块A的质量m1=2kg,物块B的质量m2=1.5kg,斜面的倾角θ=37°,斜面的长为2m,现由静止释放物块B,结果物块B在物块A的拉动下,经过3.16s运动到斜面顶端,求:
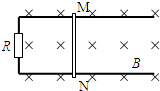 如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.
如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计. 如图所示,真空中有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2.0×10-3T,方向垂直于纸面向里,在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域,电场强度E=1.5×103N/C,在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比$\frac{q}{m}$=1.0×109C/kg带负电的粒子,粒子的运动轨迹在纸面内.一个速度方向沿y轴正方向射入磁场的粒子甲,恰能从磁场与电场的相切处进入电场.不计重力及阻力的作用.求:
如图所示,真空中有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2.0×10-3T,方向垂直于纸面向里,在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域,电场强度E=1.5×103N/C,在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比$\frac{q}{m}$=1.0×109C/kg带负电的粒子,粒子的运动轨迹在纸面内.一个速度方向沿y轴正方向射入磁场的粒子甲,恰能从磁场与电场的相切处进入电场.不计重力及阻力的作用.求:
 如图所示,AB为半径为R的金属导轨,a,b为分别沿导轨上下两表面做圆周运动的小球,要使小球不致脱离导轨,则a,b在导轨最高点的速度va,vb应满足什么条件?
如图所示,AB为半径为R的金属导轨,a,b为分别沿导轨上下两表面做圆周运动的小球,要使小球不致脱离导轨,则a,b在导轨最高点的速度va,vb应满足什么条件?