题目内容
15.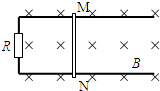 如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.
如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.(1)若用一平行于导轨的恒定拉力F拉动导体棒沿导轨向右运动,在运动过程中保持导体棒与导轨垂直,求导体棒最终的速度;
(2)若导体棒的初速度为v0,导体棒向右运动L停止,求此过程导体棒中产生的焦耳热;
(3)若磁场随时间均匀变化,磁感应强度B=B0+kt(k>0),开始导体棒静止,从t=0 时刻起,求导体棒经过多长时间开始运动以及运动的方向.
分析 (1)有法拉第电磁感应定律E=BLv和欧姆定律I=$\frac{E}{R}$,结合F安=BIL及牛顿第二定律求解.
(2)有能量守恒定律求解.
(3)有法拉第电磁感应定律求得感应电动势E=BLv,再由欧姆定律求得电流I=$\frac{E}{R}$,导体棒开始运动棒所受安培力和摩擦力相等,再由右手定则判定电流方向,由左手定则判定运动的方向.
解答 解:(1)导体棒最终匀速运动,设最终速度为v,由法拉第电磁感应定律得:E=BLv,欧姆定律得:$I=\frac{E}{2R}$,由牛顿第二定律:F=μmg+BIL,
解得:$v=\frac{2(F-μmg)R}{{{B^2}{L^2}}}$,
(2)由能量守恒定律得:$\frac{1}{2}m{v_0}^2=μmgL+Q$
回路中产生的总焦耳热$Q=\frac{1}{2}m{v_0}^2-μmgL$,
根据串并联电路特点,棒上焦耳热和电阻上焦耳热相等,
解得:${Q_棒}=\frac{1}{4}m{v_0}^2-\frac{1}{2}μmgL$
(3)磁感应强度B=B0+kt,由法拉第电磁感应定律得:$E=\frac{△B}{△t}{L^2}=k{L^2}$,欧姆定律得:$I=\frac{E}{2R}$=$\frac{k{L}^{2}}{2R}$
导体棒恰好运动时,由牛顿第二定律(B0+kt)IL=μmg,即:$({B}_{0}+kt)\frac{k{L}^{2}}{2R}L=μmg$
解得:$t=\frac{2μmgR}{{{k^2}{L^3}}}-\frac{B_0}{k}$
由楞次定律得导体棒将向左运动
答:(1)导体棒最终的速度为$\frac{2(F-μmg)R}{{B}^{2}{L}^{2}}$;
(2)此过程导体棒中产生的焦耳热为$\frac{1}{4}m{v}_{0}^{2}-\frac{1}{2}μmgL$;
(3)导体棒经过$\frac{2μmgR}{{K}^{2}{L}^{3}}-\frac{{B}_{0}}{K}$时间开始向左运动.
点评 本题考查了求速度、时间、电阻产生的热量,本题难度不大,应用E=BLv、欧姆定律、安培力公式、牛顿第二定律即可正确解题.

 小学课时特训系列答案
小学课时特训系列答案 “嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )
“嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( )| A. | 卫星在轨道Ⅲ上运动的速度等于月球的第一宇宙速度 | |
| B. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 | |
| C. | 卫星在轨道Ⅲ上运动的加速度大于沿轨道Ⅰ运动到P点时的加速度 | |
| D. | Ⅰ、Ⅱ、Ⅲ三种轨道运行相比较,卫星在轨道Ⅲ上运行的机械能最小 |

 如图所示,闭合的单匝线圈放在匀强磁场中,以角速度ω=300rad/s绕中心轴oo′逆时针匀速转动(沿oo′方向看).oo′轴垂直磁场方向.线圈的ab边长为0.1m,bc边长为0.2m,线圈的总电阻R=0.05Ω,B=0.5T.从中性面开始转动,求:
如图所示,闭合的单匝线圈放在匀强磁场中,以角速度ω=300rad/s绕中心轴oo′逆时针匀速转动(沿oo′方向看).oo′轴垂直磁场方向.线圈的ab边长为0.1m,bc边长为0.2m,线圈的总电阻R=0.05Ω,B=0.5T.从中性面开始转动,求: 如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求:
如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求: 如图所示,光滑水平轨道左端与长L=1.25m的水平传送带AB相接,传送带逆时针匀速转动的速度υ0=1m/s.轻弹簧右端固定,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进人竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,长木板与水平地面间动摩擦因数μ3=0.026,g取10m/s2.求:
如图所示,光滑水平轨道左端与长L=1.25m的水平传送带AB相接,传送带逆时针匀速转动的速度υ0=1m/s.轻弹簧右端固定,弹簧处于自然状态时左端恰位于A点.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进人竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板上掉下.半圆轨道的半径R=0.4m,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,长木板与水平地面间动摩擦因数μ3=0.026,g取10m/s2.求:

 如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.
如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.