题目内容
14.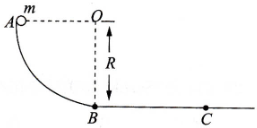 AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平直轨相切,如图所示.一可视为质点的小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,小球与水平直轨的滑动摩擦因素为?,最终小球在C点处停住(不计空气阻力).求:
AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平直轨相切,如图所示.一可视为质点的小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,小球与水平直轨的滑动摩擦因素为?,最终小球在C点处停住(不计空气阻力).求:(1)小球下滑到B点时速度的大小;
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力FB、FC各是多大?
(3)BC之间的距离.
分析 (1)对A到B的过程运用动能定理,求出小球下滑到达B点的速度大小.
(2)根据牛顿第二定律求出在B点受到的支持力大小,根据平衡求出C点受到的支持力大小.
(3)对全过程运用动能定理,求出BC间的距离.
解答 解:(1)根据动能定理得:mgR=$\frac{1}{2}m{v}^{2}$,
解得:v=$\sqrt{2gR}$.
(2)小球经过圆弧轨道的B点时有:
${F}_{B}-mg=m\frac{{v}^{2}}{R}$,
解得:FB=3mg,
小球在水平轨道的C点时:Fc=mg.
(3)对全过程运用动能定理得:mgR-μmgs=0
解得:s=$\frac{R}{μ}$.
答:(1)小球下滑到B点时速度的大小为$\sqrt{2gR}$;
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力FB、FC各是3mg,mg.
(3)BC之间的距离为$\frac{R}{μ}$.
点评 本题考查了牛顿第二定律和动能定理的综合运用,运用动能定理解题,关键选择好研究的过程,分析过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.最先在实验室内测出引力常量G大小的物理学家是( )
| A. | 开普勒 | B. | 牛顿 | C. | 卡文迪许 | D. | 爱因斯坦 |
9. 某实验小组用如图所示的实验装置来验证楞次定律.当条形磁铁自上而下穿过固定的线圈时,通过电流计的感应电流方向是( )
某实验小组用如图所示的实验装置来验证楞次定律.当条形磁铁自上而下穿过固定的线圈时,通过电流计的感应电流方向是( )
 某实验小组用如图所示的实验装置来验证楞次定律.当条形磁铁自上而下穿过固定的线圈时,通过电流计的感应电流方向是( )
某实验小组用如图所示的实验装置来验证楞次定律.当条形磁铁自上而下穿过固定的线圈时,通过电流计的感应电流方向是( )| A. | 先b→G→a,后a→G→b | B. | 先a→G→b,后b→G→a | C. | b→G→a | D. | a→G→b |
19. 如图所示,a、b为竖直向上的电场线上的两点,间距为h,一质量为m,带电荷量为q的带电质点在a点由静止释放,沿着电场线向上运动到b点恰好速度为零.下列说法正确的是( )
如图所示,a、b为竖直向上的电场线上的两点,间距为h,一质量为m,带电荷量为q的带电质点在a点由静止释放,沿着电场线向上运动到b点恰好速度为零.下列说法正确的是( )
 如图所示,a、b为竖直向上的电场线上的两点,间距为h,一质量为m,带电荷量为q的带电质点在a点由静止释放,沿着电场线向上运动到b点恰好速度为零.下列说法正确的是( )
如图所示,a、b为竖直向上的电场线上的两点,间距为h,一质量为m,带电荷量为q的带电质点在a点由静止释放,沿着电场线向上运动到b点恰好速度为零.下列说法正确的是( )| A. | 带电质点在两点所受到的电场力都是竖直向上的 | |
| B. | a点的电势比b点的电势高$\frac{mgh}{q}$ | |
| C. | 带电质点在a点的电势能比在b点的电势能小 | |
| D. | 带电质点受到的电场力比重力大 |
6. 如图所示,实线为电场线,虚线为等势线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC,则下列关系中正确的有( )
如图所示,实线为电场线,虚线为等势线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC,则下列关系中正确的有( )
 如图所示,实线为电场线,虚线为等势线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC,则下列关系中正确的有( )
如图所示,实线为电场线,虚线为等势线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC,则下列关系中正确的有( )| A. | φA>φB>φC | B. | EA>EB>EC | C. | UAB<UBC | D. | UAB=UBC |
4.关于电磁场和电磁波,下列说法中正确的是( )
| A. | 电磁波可以在真空中传播 | |
| B. | 电场随时间变化时一定产生电磁波 | |
| C. | 变化的磁场一定产生变化的电场 | |
| D. | 麦克斯韦第一次用实验证实了电磁波的存在 |
 一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a.棱镜材料的折射率为n=$\sqrt{2}$.在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜,求:光线从棱镜射出时,出射点的位置(不考虑光线沿原来路返回的情况).
一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a.棱镜材料的折射率为n=$\sqrt{2}$.在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜,求:光线从棱镜射出时,出射点的位置(不考虑光线沿原来路返回的情况).
 如图,在光滑的水平面上停放有一长木板A,A的左端放有一质量与A的质量相同的小滑块B.在将A固定(A不能滑动)和不固定(A能自由滑动)两种情况下,给B施一大小均为F=4.7N的水平向右的拉力,使B由静止开始向右运动,测得在A不固定时B滑至A的右端所用的时间是在A固定情况下B滑至A的右端所用的时间的1.2倍,求A、B之间滑动摩擦力的大小是多少?
如图,在光滑的水平面上停放有一长木板A,A的左端放有一质量与A的质量相同的小滑块B.在将A固定(A不能滑动)和不固定(A能自由滑动)两种情况下,给B施一大小均为F=4.7N的水平向右的拉力,使B由静止开始向右运动,测得在A不固定时B滑至A的右端所用的时间是在A固定情况下B滑至A的右端所用的时间的1.2倍,求A、B之间滑动摩擦力的大小是多少?