题目内容
13. 如图所示,某光滑斜面倾角为30°,其上方存在平行斜面向下的匀强电场,将一轻弹簧一端固定在斜面底端,现用一质量为m,带正电的绝缘物体将弹簧压缩锁定在A 点,解除锁定后,物体将沿斜面上滑,物体在运动过程中所能到达的最高点B距A点的竖直高度为h,物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g.则下列说法正确的是( )
如图所示,某光滑斜面倾角为30°,其上方存在平行斜面向下的匀强电场,将一轻弹簧一端固定在斜面底端,现用一质量为m,带正电的绝缘物体将弹簧压缩锁定在A 点,解除锁定后,物体将沿斜面上滑,物体在运动过程中所能到达的最高点B距A点的竖直高度为h,物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g.则下列说法正确的是( )| A. | 弹簧的最大弹性势能为mgh | |
| B. | 物体从A点运动到B点的过程中系统损失的机械能为mgh | |
| C. | 物体的最大动能等于弹簧的最大弹性势能 | |
| D. | 物体到达B点时增加的电势能为mgh |
分析 根据牛顿第二定律求出电场力的大小,根据能量守恒求出弹簧的最大弹性势能.当物体的加速度为零时,物体的动能最大.根据除重力或弹力以外其它力做功等于机械能的增量得出系统损失的机械能.结合电场力做功判断电势能的变化.
解答 解:A、在上滑到最高点的过程中,弹性势能转化为重力势能和电势能,可知弹簧的最大弹性势能大于mgh.故A错误.
BD、根据牛顿第二定律得,上滑时的加速度a=$\frac{mgsin30°+qE}{m}$,解得:qE=$\frac{1}{2}$mg.除重力或弹力以外,其它力做功等于机械能的增量,从A到B,电场力做功为W=-qEs=-mgh,则系统机械能损失mgh.电场力做功等于电势能的减小量,则电势能增加mgh.故BD正确.
C、当物体所受的合力为零,即重力的分力和电场力的合力等于弹簧的弹力,此过程中,弹簧的弹性势能转化为物体的动能和重力势能以及电势能之和,且弹簧还处于压缩状态,则物体的最大动能小于弹簧的最大弹性势能.故C错误.
故选:BD.
点评 解决本题的关键通过上滑的加速度等于g,根据牛顿第二定律求出电场力的大小,结合能量守恒定律进行分析.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
4. 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )| A. | 减小狭缝间的距离 | B. | 增大磁场的磁感应强度 | ||
| C. | 增大D形金属盒的半径 | D. | 增大匀强电场间的加速电压 |
1.真空中有两个静止的点电荷,它们之间静电力的大小为F.若保持这两个点电荷之间的距离不变,将其中一个点电荷的电荷量变为原来的一半,另一个点电荷的电荷量变为原来的两倍,则改变电荷量后这两个点电荷之间静电力的大小为( )
| A. | 2F | B. | F | C. | $\frac{F}{2}$ | D. | $\frac{F}{4}$ |
8.在电场中某点放入电荷量为q的正检验电荷时,该点的场强大小为E,若在该点放入电荷量q′=-2q的负检验电荷,该点的场强大小为E′,则有( )
| A. | E′=E,方向与E相同 | B. | E′=E,方向与E相反 | ||
| C. | E′=$\frac{E}{2}$,方向与E相反 | D. | E′=2E,方向与E相同 |
5.下面为四个质点的图象,其中反映质点做匀加速直线运动的是( )
| A. |  | B. |  | C. |  | D. |  |
3.以下说法中正确的是( )
| A. | 因为力是物体对物体的作用,所以只有相互接触的物体间才有力的作用 | |
| B. | 某物体重心的位置必然在该物体上 | |
| C. | 受静摩擦力作用的物体有可能是运动的 | |
| D. | 物体所受滑动摩擦力的方向与物体运动的方向必然相反 |
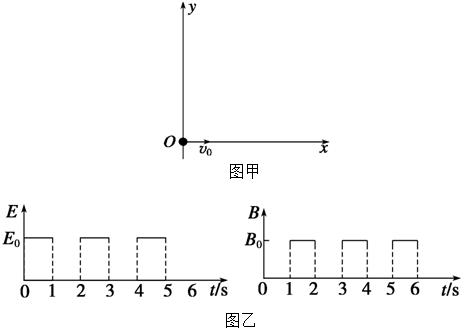 如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求: