题目内容
3.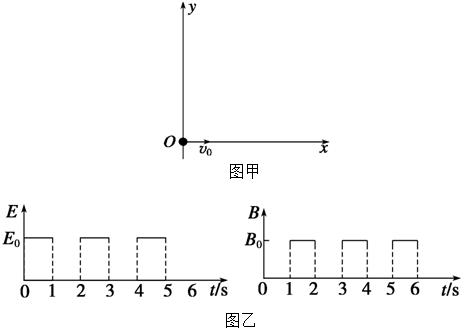 如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:(1)t=1s末时,小球速度的大小和方向;
(2)在1s~2s这段时间内,金属小球在磁场中做圆周运动的半径和周期;
(3)在3s~4s这段时间内,金属小球运动至离x轴最远点的位置坐标.
分析 (1)第一秒内粒子做类似平抛运动,根据牛顿第二定律和运动学公式列式求解;
(2)根据洛伦兹力提供向心力列式求解轨道半径,由圆周运动公式求得周期;
(3)粒子奇数秒内做类似平抛运动,偶数秒内做匀速圆周运动,轨道半径逐渐增大,画出轨迹.求出3s末的位置坐标.
解答 解:(1)第一秒内:小球做类平抛运动,
vx=v0,vy=at=$\frac{q{E}_{0}}{m}$t,
速度为:v1=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$,tanθ=$\frac{{v}_{y}}{{v}_{x}}$,
解得:v1=2$\sqrt{2}$m/s,θ=45°,与x轴正方向夹角为45°;
(2)1s-2s内小球做匀速圆周运动,由牛顿第二定律得:
qv1Bm=$\frac{{v}^{2}}{{R}_{1}}$,
解得:R1=$\frac{\sqrt{2}}{π}$m,
周期为:T=$\frac{2πR}{v}$,解得:T=1s;
(3)粒子运动轨迹如图甲所示,3s末粒子的坐标为:x=v0t=2×2=4m,
y=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{q{E}_{0}}{m}$t2=$\frac{1}{2}$×$\frac{0.1×0.2}{0.01}$×22=4m,
此时粒子的速度为:v3=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{v}_{0}^{2}+(\frac{q{E}_{0}}{m}t)^{2}}$,tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\frac{q{E}_{0}}{m}t}{{v}_{0}}$,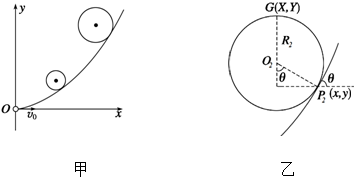 解得:v3=2$\sqrt{5}$m/s,tanθ=2,带电粒子在3s~4s内做圆周运动的轨迹如图乙所示
解得:v3=2$\sqrt{5}$m/s,tanθ=2,带电粒子在3s~4s内做圆周运动的轨迹如图乙所示
半径:R2=$\frac{m{v}_{3}}{q{B}_{0}}$=$\frac{0.01×2\sqrt{5}}{0.1×0.2π}$=$\frac{\sqrt{5}}{π}$m;
3s~4s内粒子运动至离x轴最远点G坐标为(X,Y)
X=x-R2sinθ=4+$\frac{\sqrt{5}}{π}$sinθ=(4-$\frac{2}{π}$)m,Y=y+R2(1+cosθ)=4+$\frac{\sqrt{5}}{π}$(1+cosθ)=(4+$\frac{\sqrt{5}}{π}$+$\frac{1}{π}$)m;
答:(1)t=1s末时,小球速度的大小为:2$\sqrt{2}$m/s,方向:与x轴正方向夹角为45°;
(2)在1s~2s这段时间内,金属小球在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{π}$m,周期为1s;
(3)在3s~4s这段时间内,金属小球运动至离x轴最远点的位置坐标为:((4-$\frac{2}{π}$)m,(4+$\frac{\sqrt{5}}{π}$+$\frac{1}{π}$)m).
点评 本题中粒子奇数秒内做类似平抛运动,偶数秒内做匀速圆周运动,关键是画出运动轨迹并根据平抛运动规律和匀速圆周运动规律列式分析.

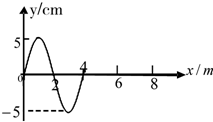
| A. | 当波传到6处时,质点6作简谐运动,但振幅小于5cm | |
| B. | 当波传到6处时,质点2的振动方向向上 | |
| C. | 各质点的振动频率均不一样 | |
| D. | 当质点2振动80次时,质点6振动79次 |
| A. | 都等于F | B. | 逐渐增大 | C. | 逐渐减小 | D. | 都等于零 |
 物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )| A. | μA>μB,mA<mB | B. | μA<μB,mA<mB | C. | μA>μB,mA>mB | D. | μA<μB,mA>mB |
 如图所示,某光滑斜面倾角为30°,其上方存在平行斜面向下的匀强电场,将一轻弹簧一端固定在斜面底端,现用一质量为m,带正电的绝缘物体将弹簧压缩锁定在A 点,解除锁定后,物体将沿斜面上滑,物体在运动过程中所能到达的最高点B距A点的竖直高度为h,物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g.则下列说法正确的是( )
如图所示,某光滑斜面倾角为30°,其上方存在平行斜面向下的匀强电场,将一轻弹簧一端固定在斜面底端,现用一质量为m,带正电的绝缘物体将弹簧压缩锁定在A 点,解除锁定后,物体将沿斜面上滑,物体在运动过程中所能到达的最高点B距A点的竖直高度为h,物体离开弹簧后沿斜面向上运动的加速度大小等于重力加速度g.则下列说法正确的是( )| A. | 弹簧的最大弹性势能为mgh | |
| B. | 物体从A点运动到B点的过程中系统损失的机械能为mgh | |
| C. | 物体的最大动能等于弹簧的最大弹性势能 | |
| D. | 物体到达B点时增加的电势能为mgh |
 如图所示,放在斜面上的长木板B的上表面是光滑的,给B一个沿斜面向下的初速度v0,B沿斜面匀速下滑.在B下滑的过程中,在B的上端轻轻地放上物体A,若两物体的质量均为m,斜面倾角为θ,则B的加速度大小为gsinθ,方向为沿斜面向上;当A的速度为 $\frac{3}{2}$v0时(设该时A没有脱离B,B也没有到达斜面底端),B的速度为0.
如图所示,放在斜面上的长木板B的上表面是光滑的,给B一个沿斜面向下的初速度v0,B沿斜面匀速下滑.在B下滑的过程中,在B的上端轻轻地放上物体A,若两物体的质量均为m,斜面倾角为θ,则B的加速度大小为gsinθ,方向为沿斜面向上;当A的速度为 $\frac{3}{2}$v0时(设该时A没有脱离B,B也没有到达斜面底端),B的速度为0.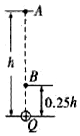 如图所示,Q为固定的正点电荷,A、B两点在Q的正上方与Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度正好又变为零,若此电荷在A点处的加速度大小为$\frac{3}{4}$g,试求:
如图所示,Q为固定的正点电荷,A、B两点在Q的正上方与Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度正好又变为零,若此电荷在A点处的加速度大小为$\frac{3}{4}$g,试求:
 如图所示,用长为L=10cm的绝缘细线拴住一个质量为m=0.1kg,带电量为q=$\sqrt{3}×{10^{-2}}$C的小球,线的另一端拴在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平方向成60°角且到达B点时,小球的速度正好为零.g取10m/s2.求:(结果保留一位有效数字)
如图所示,用长为L=10cm的绝缘细线拴住一个质量为m=0.1kg,带电量为q=$\sqrt{3}×{10^{-2}}$C的小球,线的另一端拴在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平方向成60°角且到达B点时,小球的速度正好为零.g取10m/s2.求:(结果保留一位有效数字)