题目内容
6. 一平台的局部如图甲所示,水平面为光滑,竖直面为粗糙,右角上固定一定滑轮,在水平面上放着一质量mA=2.0kg,厚度可忽略不计的薄板A,薄板A长度L=1.5m,在板A上叠放着质量mB=1.0kg,大小可忽略的物块B,物块B与板A之间的动摩擦因数为μ=O.6,一轻绳绕过定滑轮,轻绳左端系在物块B上,右端系住物块C,物块C刚好可与竖直面接触.起始时令各物体都处于静止状态,绳被拉直,物块B位于板A的左端点,然后放手,设板A的右端距滑轮足够远,台面足够高,最大静摩擦力等于滑动摩擦力,忽略滑轮质量及其与轴之间的摩擦,g取10m/s2,求
一平台的局部如图甲所示,水平面为光滑,竖直面为粗糙,右角上固定一定滑轮,在水平面上放着一质量mA=2.0kg,厚度可忽略不计的薄板A,薄板A长度L=1.5m,在板A上叠放着质量mB=1.0kg,大小可忽略的物块B,物块B与板A之间的动摩擦因数为μ=O.6,一轻绳绕过定滑轮,轻绳左端系在物块B上,右端系住物块C,物块C刚好可与竖直面接触.起始时令各物体都处于静止状态,绳被拉直,物块B位于板A的左端点,然后放手,设板A的右端距滑轮足够远,台面足够高,最大静摩擦力等于滑动摩擦力,忽略滑轮质量及其与轴之间的摩擦,g取10m/s2,求(1)若物块C质量mc=1.0kg,推理判断板A和物块B在放手后是否保持相对静止;
(2)若物块C质量mc′=3.0kg,从放手开始计时,经过去t=2.Os,物块C下降的高度;
(3)若物块C质量mc=1.0kg,固定住物块B,物块C静止,现剪断轻绳,同时也对物块C施加力F,方向水平向左,大小随时间变化如图乙所示,断绳时刻开始计时,经过t′=2.Os,物块C恰好停止运动,求物块C与竖直面之间的动摩擦因数和此过程中的最大速度.
分析 (1)对ABC整体研究,假设一起运动,根据牛顿第二定律求出加速度,再隔离分析求出AB间的摩擦力,与最大静摩擦力比较,判断是否保持相对静止.
(2)通过整体隔离分析得出A与B发生相对滑动,根据牛顿第二定律分别求出A、B的加速度,结合运动学公式进行求解.
(3)通过牛顿第二定律得出C加速度的表达式,作出图线,结合图线与时间轴围成的面积进行求解.
解答 解:(1)设ABC一起运动,以ABC为系统,根据牛顿第二定律: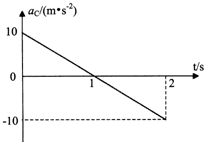
mCg=(mA+mB+mC)a1,
代入数据解得:a1=2.5m/s2,
对A,根据牛顿第二定律:f=mAa1=2×2.5N=5N,
AB间最大静摩擦力:fm=μmBg=6.0N,
由于f<fm,假设成立,A与B相对静止.
(2)设ABC一起运动,以ABC为系统,根据牛顿第二定律有:
mC′g=(mA+mB+mC′)a2,
代入数据解得:a2=5.0m/s2
对A,根据牛顿第二定律得:f′=mAa2=2×5N=10N,
由于f′>fm,假设不成立,A与B相对滑动.
对A,根据牛顿第二定律,μmBg=mAaA,代入数据解得:aA=3.0m/s2,
对BC为系统,根据牛顿第二定律:
mC′g-μmBg=(mB+mC′)aB,
代入数据解得:aB=6.0m/s2.
设经t1时间B运动到A的右端,则有:$\frac{1}{2}$aBt12-$\frac{1}{2}$aAt12=L,
代入数据解得:t1=1.0s.
B第一段的位移:${s}_{1}=\frac{1}{2}{a}_{B}{t}_{1}^{2}$=$\frac{1}{2}×6×1m=3m$.
经t1时间B运动的速度:v1=aBt1=6×1m/s=6m/s,
B在光滑平面上滑动,对BC为系统,根据牛顿第二定律:
mC′g=(mB+mC′)aB′,
代入数据解得:a′B=7.5m/s2,
B第二段的位移为:${s}_{2}={v}_{1}(t-{t}_{1})+\frac{1}{2}{a}_{B}(t-{t}_{1})^{2}$,
代入数据解得:s2=9.75m,
物块C下降的高度:h=s1+s2=3+9.75m=12.75m.
(3)设C与竖直面的动摩擦因数为μ′,
令k=20N/s,
根据图乙可得,F=kt,
对C水平方向:N=F,
C受摩擦力fC=μ′N,
以C为对象,有:mCg-fC=mCaC,
联立解得:${a}_{C}=g-\frac{μ′kt}{{m}_{C}}$=(10-20μ′t)m/s2,
由上式可得如图的图象,t=t′=2s,物块v=0,则:aC=-10m/s2,
代入数据解得:μ′=0.5.
由图可知t=1s时速度最大,最大速度等于图线与坐标轴围成的面积,有:
${v}_{m}=\frac{1}{2}×1×10m/s=5m/s$.
答:(1)A与B相对静止.
(2)物块C下降的高度为12.75m.
(3)物块C与竖直面之间的动摩擦因数为0.5,此过程中的最大速度为5m/s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,涉及多过程问题,难度较大,综合性较强,关键理清物体的运动规律,结合牛顿第二定律和运动学公式进行求解.对于第三问,得出C的加速度表达式是关键,知道a-t图线围成的面积表示速度的变化量.

 北京时间2013年4月20日8时02分四川省雅安市芦山县发生7.0级地震.当地群众生活困难,一方有难八方支援.有这样一辆运送救灾物资的货车装满了土豆,如图所示,以一定的初速度在摩擦因数为μ的水平地面上做匀减速运动,不计其它外力及空气阻力,则中间一质量为m的土豆A受到其它土豆对它的总作用力大小应是( )
北京时间2013年4月20日8时02分四川省雅安市芦山县发生7.0级地震.当地群众生活困难,一方有难八方支援.有这样一辆运送救灾物资的货车装满了土豆,如图所示,以一定的初速度在摩擦因数为μ的水平地面上做匀减速运动,不计其它外力及空气阻力,则中间一质量为m的土豆A受到其它土豆对它的总作用力大小应是( )| A. | μmg | B. | mg $\sqrt{1-{μ}^{2}}$ | C. | mg $\sqrt{1+{μ}^{2}}$ | D. | mg$\sqrt{{μ}^{2}-1}$ |
 质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v-t图线.由图线可知( )
质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v-t图线.由图线可知( )| A. | 图线a反映了物体受水平拉力的作用 | |
| B. | 图线b反映了物体受水平拉力的作用 | |
| C. | 水平拉力为1.8N | |
| D. | 水平拉力为1.2N |

| A. | 小球在x=L处的速度最大 | |
| B. | 小球一定可以到达x=-2L点处 | |
| C. | 小球在x=0点受到电场力方向向右 | |
| D. | 固定在AB处的电荷的电量之比为QA:QB=4:1 |
 我校经纬楼楼顶有一半圆型建筑,如图1所示,顶部有一设施出现问题,工人(图中小物块)上去维修,在从A经顶部缓慢移动至另一侧A′的过程中,则图象2反映的是该过程中( )
我校经纬楼楼顶有一半圆型建筑,如图1所示,顶部有一设施出现问题,工人(图中小物块)上去维修,在从A经顶部缓慢移动至另一侧A′的过程中,则图象2反映的是该过程中( )| A. | 重力随时间变化的规律 | B. | 支持力随时间变化的规律 | ||
| C. | 摩擦力随时间变化的规律 | D. | 合外力随时间变化的规律 |
 两个共力点F1、F2的大小不变,它们的合力F与两力F1、F2之间的夹角θ的关系如图所示,求F1、F2的大小及合力F的大小变化范围.
两个共力点F1、F2的大小不变,它们的合力F与两力F1、F2之间的夹角θ的关系如图所示,求F1、F2的大小及合力F的大小变化范围. 如图所示,倾角θ=37°的斜面固定在水平面上.质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动.小物块与斜面间的动摩擦因数μ=0.25(斜面足够长,取g=10m/s2.sin37°=0.6,cos37°=0.8)
如图所示,倾角θ=37°的斜面固定在水平面上.质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动.小物块与斜面间的动摩擦因数μ=0.25(斜面足够长,取g=10m/s2.sin37°=0.6,cos37°=0.8) 如图所示,一水平传送带AB长为L=6m,离水平地面的高为h=5m,地面上C点在传送带右端点B的正下方.一物块以水平初速度v0=4m/s自A点滑上传送带,传送带匀速转动,物块与传送带间的动摩擦因数为μ=0.2,重力加速度为g=10m/s2.
如图所示,一水平传送带AB长为L=6m,离水平地面的高为h=5m,地面上C点在传送带右端点B的正下方.一物块以水平初速度v0=4m/s自A点滑上传送带,传送带匀速转动,物块与传送带间的动摩擦因数为μ=0.2,重力加速度为g=10m/s2.