题目内容
5.土星拥有许多卫星,至目前为止所发现的卫星数已经有30个,下表是土星部分卫星的相关数据.| 土星的卫星 | 名称 | 直径(km) | 质量(kg) | 平均轨道半径(km) | 发现年份 |
| 土卫一 | 美马斯 | 392 | 3.80×1019 | 185520 | 1789年 |
| 土卫二 | 恩克拉多斯 | 498 | 7.30×1019 | 238020 | 1789年 |
| 土卫三 | 特提斯 | 1060 | 6.22×1020 | 294660 | 1684年 |
| 土卫四 | 狄俄涅 | 1120 | 1.05×1021 | 377400 | 1684年 |
| 土卫五 | 雷亚 | 1530 | 2.49×1021 | 527040 | 1672年 |
| 土卫六 | 泰坦 | 5150 | 1.35×1023 | 1221830 | 1655年 |
| A. | “狄俄涅”绕土星运动的周期大于“泰坦”绕土星运动的周期 | |
| B. | “泰坦”绕土星运动的加速度大于“美马斯”绕土星运动的加速度 | |
| C. | “特提斯”绕土星运动的线速度大于“雷亚”绕土星运动的线速度 | |
| D. | “狄俄涅”绕土星运动的角速度大于“恩克拉多斯”绕土星运动的角速度 |
分析 对于卫星,万有引力提供向心力,根据牛顿第二定律列式求解出周期、加速度、线速度、角速度的表达式进行分析比较即可.
解答 解:A、对卫星,根据牛顿第二定律,有:
$G\frac{Mm}{r^2}=m\frac{{4{π^2}}}{T^2}r$
解得:
$T=2π\sqrt{\frac{r^3}{GM}}$
“狄俄涅”的轨道半径小于“泰坦”的轨道半径,故“狄俄涅”的周期小于“泰坦”周期,故A错误;
B、对卫星,根据牛顿第二定律,有:
$G\frac{Mm}{r^2}=ma$
解得:
a=$\frac{GM}{{r}^{2}}$
“泰坦”的轨道半径大于“美马斯”的轨道半径,故“泰坦”绕土星运动的加速度小于“美马斯”绕土星运动的加速度
故B错误;
C、对卫星,根据牛顿第二定律,有:
$G\frac{Mm}{r^2}=m\frac{v^2}{r}$
解得:
v=$\sqrt{\frac{GM}{r}}$
“特提斯”绕土星运动的轨道半径小于“雷亚”绕土星运动的轨道半径,故“特提斯”绕土星运动的线速度大于“雷亚”绕土星运动的线速度,故C正确;
D、对卫星,根据牛顿第二定律,有:
$G\frac{Mm}{r^2}=m{ω^2}r$
解得:
$ω=\sqrt{\frac{GM}{r^3}}$
“特提斯”绕土星运动的轨道半径小于“雷亚”绕土星运动的轨道半径,故“特提斯”绕土星运动的角速度大于“雷亚”绕土星运动的角速度,故D错误;
故选:C
点评 本题关键是明确卫星的动力学原理,根据万有引力定律和牛顿第二定律列式求解出各个运动学参量的表达式进行分析即可.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
9.在“探究单摆周期与摆长关系”的实验中,下列做法正确的是 ( )
| A. | 应选择伸缩性小、尽量长些的细线做摆线 | |
| B. | 用刻度尺测出细线的长度并记为摆长l | |
| C. | 在小偏角下让单摆从静止开始摆动 | |
| D. | 当单摆经过平衡位置时开始计时,测量一次全振动的时间作为单摆的周期T | |
| E. | 分析实验数据,若认为周期与摆长的关系为T2∝l,则可作T2-l图象;如果图象是一条直线,则关系T2∝l成立 |
10.如图所示,两木块A、B叠放在水平桌面上,今以水平拉力F拉B没拉动,则以下说法中正确的是( )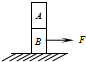

| A. | A、B间不存在摩擦力作用 | |
| B. | A、B间有静摩擦力作用 | |
| C. | B与桌面间没有相对运动的趋势 | |
| D. | 保证A、B仍然相对地面静止的情况下,加大拉力F后,则A与B之间可能产生摩擦力 |
17.以下关于运动的描述正确的是( )
| A. | 在研究芭蕾舞演员的精彩舞姿时,可以把演员看作质点 | |
| B. | “3点20分”与“3个小时20分钟”分别指时刻和时间间隔 | |
| C. | “坐地日行三万里”是以地面为参考系 | |
| D. | 速度、位移、加速度、时刻是矢量,时间间隔、速率是标量 |
14.下列物理量中,属于矢量的是( )
| A. | 电势 | B. | 电势差 | C. | 电势能 | D. | 电场强度 |
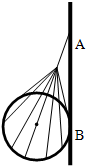 在光滑墙壁上用网兜把足球挂在A点,足球与墙面的接触点为B.足球的质量为0.4kg,绳与墙壁的夹角为37°.(sin37°=0.6,cos37°=0.8)
在光滑墙壁上用网兜把足球挂在A点,足球与墙面的接触点为B.足球的质量为0.4kg,绳与墙壁的夹角为37°.(sin37°=0.6,cos37°=0.8)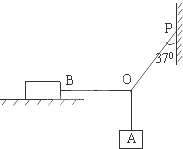 如图所示,质量为mB=6kg的物体B放在粗糙的水平桌面上,他们之间的动摩擦因数μ=0.4,质量为mA=2kg的物体A与物体B都处于静止状态,细绳OB呈水平,细绳OP与竖直方向成37°角.已知OA、OB、OP三细绳所能承受的最大张力都是30N,(sin37°=0.6,cos37°=0.8).求:
如图所示,质量为mB=6kg的物体B放在粗糙的水平桌面上,他们之间的动摩擦因数μ=0.4,质量为mA=2kg的物体A与物体B都处于静止状态,细绳OB呈水平,细绳OP与竖直方向成37°角.已知OA、OB、OP三细绳所能承受的最大张力都是30N,(sin37°=0.6,cos37°=0.8).求: