��Ŀ����
18����ͼ��ʾ���������L1��ƽ�дֲڽ�������̶���ˮƽ���ϣ������Ϸֲ���n ������Ϊd�����Ϊ2d����ǿ�ų����ų�����ֱˮƽ�����ϣ��ڵ�����������һ����ֵΪR�ĵ��裬�������˾����һ���ų�����L2��λ�÷���һ������Ϊm����ΪL1����ֵΪr�Ľ�������������輰�������뵼���ĽӴ���������ƣ�ijʱ���𣬽�������һˮƽ���ҵ���֪����F�������ɾ�ֹ��ʼ�����˶�����֪�������뵼���Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg��
��1�����������ܹ�����ͨ��ÿ����ǿ�ų�������������뿪��2����ǿ�ų�����ʱ���ٶ�v2�Ĵ�С��
��2��������ڣ�1��С������ʱ�����n����ǿ�ų�����ĴŸ�Ӧǿ��Bn�Ĵ�С��
��3���ֱ��ֺ���F���䣬ʹÿ���ų�����ĴŸ�Ӧǿ�Ⱦ���ͬ�����ֽ�����ͨ��ÿ���ų�����ʱ��·�еĵ����仯������ȫ��ͬ����������ӿ�ʼ�˶���ͨ����n���ų������������������˵���R�ϲ����Ľ�����Q��
���� ��1���������ȼ����˶�ʱ������ţ�ٵڶ����ɺ��˶�ѧ��ʽ���������뿪��2����ǿ�ų�����ʱ���ٶ�v2�Ĵ�С��
��2������������ȼ����˶���λ�ƣ������˶�ѧ��ʽ��������n���ų����ٶȣ������ڵ�n���ų��е�����ƽ�����n���ų��ĴŸ�Ӧǿ��Bn��
��3�������˶�ѧ��ʽ��϶��ܶ������������·�����Ľ����ȣ�����������ϵ������ϵĽ����ȣ�
��� �⣺��1���������ȼ����˶�ʱ����ţ�ٵڶ�������
F-��mg=ma
���˶�ѧ��ʽ�� v22=2a��L2+2d��
��ã�v2=$\sqrt{\frac{2��F-��mg����{L}_{2}+2d��}{m}}$
��2���������ȼ����˶�����λ��Ϊ x=L2+2nd-2d
�����������n����ǿ�ų����ٶ����� vn2=2ax
�������ڵ�n���ų��������˶���
F-��mg-F��=0
�� F��=$\frac{{B}_{n}^{2}{L}_{1}^{2}{v}_{n}}{R+r}$
��ã�Bn=$\frac{1}{{L}_{1}}$$\root{4}{\frac{m��F-��mg����R+r��^{2}}{2{L}_{2}+4nd-4d}}$
��3������������ÿ���ų�ʱ���ٶ�v���뿪ÿ���ų�ʱ���ٶ�v�����ͬ��������ɵ�
v2=2aL2
v2-v'2=2a•2d
�������ӿ�ʼ�˶���ͨ����n���ų�����Ĺ����У���
x��=L2+3nd-2d
���ݶ��ܶ����ã�F-��mg��x��-Q��=$\frac{1}{2}$mv��2��
����R�ϲ����Ľ����� Q=$\frac{R}{R+r}$Q����
��ã�Q=$\frac{3R}{R+r}$nd��F-��mg��
��
��1���������뿪��2����ǿ�ų�����ʱ���ٶ�v2�Ĵ�С��$\sqrt{\frac{2��F-��mg����{L}_{2}+2d��}{m}}$��
��2����n����ǿ�ų�����ĴŸ�Ӧǿ��Bn�Ĵ�С��$\frac{1}{{L}_{1}}$$\root{4}{\frac{m��F-��mg����R+r��^{2}}{2{L}_{2}+4nd-4d}}$��
��3����˵���R�ϲ����Ľ�����Q��$\frac{3R}{R+r}$nd��F-��mg����
���� ������������ǻ������ؼ�������ת�����غ�Ƕ�����⣬����ʱҪע��ץסʹ��������ų����ٶȶ���ͬ���Լ�ͨ��ÿ�δų�ʱ��·�з���������ͬ��������

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| A�� | ������40 km/h�ٶ���ʻ | |
| B�� | ƽ���ٶȴ�С���ó���40 km/h | |
| C�� | ˲ʱ�ٶȴ�С���ó���40 km/h | |
| D�� | �����ϵ��ٶȼ�ָʾֵ����ʱ���ǿ��Գ���40 km/h |
 ��ͼ��ʾ������Ϊm���߳�ΪL����·����ΪR�������ν�������ϸ�ߵ�ס�����ڹ⻬�����Ϊ30���б���ϣ��ߵ���һ�˿�����������֣�����һ������ΪM��M��m�������룬��������б���Ϸ���һ�Ÿ�Ӧǿ��ΪB����ǿ�ų����ų����±߽����������ϱ�ƽ�������һ�����룮���ڽ�����ӿ�ʼ�˶������������ų��Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ������Ϊm���߳�ΪL����·����ΪR�������ν�������ϸ�ߵ�ס�����ڹ⻬�����Ϊ30���б���ϣ��ߵ���һ�˿�����������֣�����һ������ΪM��M��m�������룬��������б���Ϸ���һ�Ÿ�Ӧǿ��ΪB����ǿ�ų����ų����±߽����������ϱ�ƽ�������һ�����룮���ڽ�����ӿ�ʼ�˶������������ų��Ĺ����У�����˵����ȷ���ǣ�������| A�� | ϸ�߶Խ��������Ĺ����ڽ��������ӵĻ�е�� | |
| B�� | ϸ�߶Խ�������������ܵ���Mg | |
| C�� | �߿��ϵ��ȹ��ʿ��ܴ���$\frac{��M-o.5m��^{2}{g}^{2}R}{{B}^{2}{L}^{2}}$ | |
| D�� | ���߿���ٽ���ų���ϵͳ�Ļ�е����ʧ����С��MgL-$\frac{1}{2}$mgL |

| A�� | ��Ȧ�еĸ�Ӧ����֮��I1��I2=2��1 | |
| B�� | ��������Ȧ�ϵ�������С֮��F1��F2=1��2 | |
| C�� | ��Ȧ�в����Ľ�����֮��Q1��Q2=2��1 | |
| D�� | ͨ����Ȧijһ����ĵ����֮��q1��q2=1��2 |
 ��ͼ��ʾ�������ֱ�Ϊm1��m2������С��A��B�����е������ֵ�ɣ�ͨ����Ե�ᵯ�������ӣ����ھ�Ե�⻬��ˮƽ���ϣ�ͻȻ��һˮƽ���ҵ���ǿ�糡������A��B���ɾ�ֹ��ʼ�˶�������С��A��B�͵�����ɵ�ϵͳ���ԣ�����Ӿ�ֹ���������Ĺ����У�����˵����ȷ���ǣ������������в����ǵ�ɼ�����������ã��ҵ��ɲ����������ȣ���������
��ͼ��ʾ�������ֱ�Ϊm1��m2������С��A��B�����е������ֵ�ɣ�ͨ����Ե�ᵯ�������ӣ����ھ�Ե�⻬��ˮƽ���ϣ�ͻȻ��һˮƽ���ҵ���ǿ�糡������A��B���ɾ�ֹ��ʼ�˶�������С��A��B�͵�����ɵ�ϵͳ���ԣ�����Ӿ�ֹ���������Ĺ����У�����˵����ȷ���ǣ������������в����ǵ�ɼ�����������ã��ҵ��ɲ����������ȣ���������| A�� | ϵͳ��е�ܲ������� | B�� | ϵͳ��е���غ� | ||
| C�� | ϵͳ���ܲ������� | D�� | ϵͳ���ܲ��� |
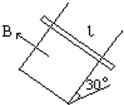 ��ͼ��ʾ�����������ˮƽ���30��ǣ���ǿ�ų��ĴŸ�ǿ��B=0.4T������ֱ���ƽ�����ϣ���������l=0.5m������Ϊ0.1N�������ڿ������Ħ���ػ����������ܵ��ܵ���Ϊ2�����˶�ʱ����Ϊ���䣬������տ�ʼ�������2m���ʣ�
��ͼ��ʾ�����������ˮƽ���30��ǣ���ǿ�ų��ĴŸ�ǿ��B=0.4T������ֱ���ƽ�����ϣ���������l=0.5m������Ϊ0.1N�������ڿ������Ħ���ػ����������ܵ��ܵ���Ϊ2�����˶�ʱ����Ϊ���䣬������տ�ʼ�������2m���ʣ�
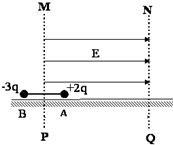 ��ͼ��ʾ���ó�ΪL�ľ�Ե�����������������Ϊm�Ĵ���С��A��B���ڹ⻬��Ե��ˮƽ���ϣ�A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ-3q������һ������ϵͳ�����Ǿ�����Ϊ�ʵ㣬Ҳ��������������õĿ�������������С��A�����н���ǿ�糡�����ڣ���֪����MPλ��ϸ�˵��д����ϣ�MP�����û�е糡���Ҳ�����ǿ�糡���糡ǿ�ȴ�СΪE������ˮƽ���ң��Ӿ�ֹ�ͷŴ���ϵͳ�������Դ���ϵͳ�˶��������������Ĵų�Ӱ�죩����
��ͼ��ʾ���ó�ΪL�ľ�Ե�����������������Ϊm�Ĵ���С��A��B���ڹ⻬��Ե��ˮƽ���ϣ�A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ-3q������һ������ϵͳ�����Ǿ�����Ϊ�ʵ㣬Ҳ��������������õĿ�������������С��A�����н���ǿ�糡�����ڣ���֪����MPλ��ϸ�˵��д����ϣ�MP�����û�е糡���Ҳ�����ǿ�糡���糡ǿ�ȴ�СΪE������ˮƽ���ң��Ӿ�ֹ�ͷŴ���ϵͳ�������Դ���ϵͳ�˶��������������Ĵų�Ӱ�죩����