题目内容
5.从距地面高为4.9m处以9.8m/s的初速度水平抛出一小球,不计空气阻力,则( )| A. | 小球落地点与抛出点的水平距离为9.8m | |
| B. | 小球落地点与抛出点的水平距离为4.9m | |
| C. | 小球落地时的速度大小为4.9m/s | |
| D. | 小球落地时的速度大小为9.8m/s |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出平抛运动的时间,结合初速度和时间求出水平位移.根据速度的合成原则求解落地时速度.
解答 解:A、根据$h=\frac{1}{2}g{t}^{2}$得:$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×4.9}{9.8}}=1s$;小球落地点与抛出点之间的水平距离:x=v0t=9.8×1m=9.8m,故A正确,B错误;
C、落地时,竖直方向速度vy=gt=9.8m/s,则小球落地时的速度大小v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=9.8\sqrt{2}m/s$,故CD错误.
故选:A
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,知道平抛运动的时间由高度决定.

练习册系列答案
相关题目
15. 某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系式为x=Asinωt,图象如图所示.则以下说法正确的是( )
某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系式为x=Asinωt,图象如图所示.则以下说法正确的是( )
 某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系式为x=Asinωt,图象如图所示.则以下说法正确的是( )
某弹簧振子在水平方向上做简谐运动,其位移x随时间t变化的关系式为x=Asinωt,图象如图所示.则以下说法正确的是( )| A. | 弹簧在第1 s末与第5 s末的长度相同 | |
| B. | 简谐运动的圆频率ω=$\frac{π}{4}$rad/s | |
| C. | 第3s末弹簧振子的位移大小为$\frac{\sqrt{2}}{2}$A | |
| D. | 第3s末至第5s末弹簧振子的速度方向都相同 |
13.质量为m的人造地球卫星在圆轨道上,它到地面的距离等于地球半径R,地面上的重力加速度为g,则( )
| A. | 卫星运行的线速度为$\sqrt{2gR}$ | B. | 卫星运行的角速度为$\sqrt{\frac{g}{8R}}$ | ||
| C. | 卫星运行的周期为4π$\sqrt{\frac{2R}{g}}$ | D. | 卫星的加速度为$\frac{1}{2}$g |
17.下列关于物体运动的说法,正确的是( )
| A. | 物体速度不为零,其加速度也一定不为零 | |
| B. | 物体加速度方向改变时,速度方向可以保持不变 | |
| C. | 物体具有加速度时,它的速度可能不会改变 | |
| D. | 物体的加速度变大时,速度也一定随之变大 |
8.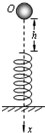 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )| A. | 弹簧的弹性势能逐渐增大 | |
| B. | 球刚接触弹簧时动能最大 | |
| C. | 全过程中小球的机械能守恒 | |
| D. | 该过程的某一阶段内,小球的动能增大而小球的机械能减少 |
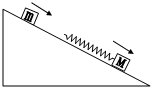 质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能.
质量m和M的两木块分别以v1和v2的速度沿粗糙足够长的斜面匀速下滑.已知斜面固定,v1>v2.求两木块发生相互作用的过程中.轻质弹簧能达到的最大弹性势能. 如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ.重力加速度为g.
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ.重力加速度为g.