题目内容
18. 如图所示,水平地面上有一个倾角α=30°,高h=1m的斜面,一个质量为m的物体从斜面底端A以v0=10m/s的速度沿斜面抛出,物体与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,不计空气阻力,g取10m/s2,问物体落回地面时的速度多大?
如图所示,水平地面上有一个倾角α=30°,高h=1m的斜面,一个质量为m的物体从斜面底端A以v0=10m/s的速度沿斜面抛出,物体与斜面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,不计空气阻力,g取10m/s2,问物体落回地面时的速度多大?
分析 从A到C整个过程,重力做功为零,摩擦力做功为-μmgScosθ,根据动能定理求解物体落到C时的速度大小.
解答 解:从A到C整个过程,重力做功为零,根据动能定理得:
-μmgScosθ=$\frac{1}{2}$mv${\;}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
即$-\frac{\sqrt{3}}{3}$×$m×10×2×\frac{\sqrt{3}}{2}$=$\frac{1}{2}m{v}_{C}^{2}$$-\frac{1}{2}m×1{0}^{2}$
解得:vC=4$\sqrt{5}$m/s
答:
物体落到C时的速度大小为4$\sqrt{5}$m/s
点评 本题是两个过程问题,第一个过程,物体做匀减速运动,第二过程斜抛运动,对全过程运用动能定理求解物体落地速度的大小.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
8.一质量为M的平板车以速度v在光滑水平面上滑行,质量为m的烂泥团从离车h高处自由下落,恰好落到车面上,则小车的速度大小是( )
| A. | 仍是v | B. | $\frac{Mv}{m+M}$ | C. | $\frac{m\sqrt{2gh}}{m+M}$ | D. | $\frac{mv+m\sqrt{2gh}}{m+M}$ |
6.物体在位于同一平面内的三个共点力作用下静止,其中两个力的大小分别为F1=10N,F2=8N.若第三个力与F1的正向夹角为θ,则θ可能为( )
| A. | 60° | B. | 120° | C. | 150° | D. | 180° |
13.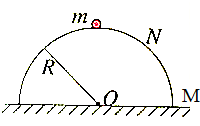 如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
 如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )| A. | 沿球面下滑至最低点M | |
| B. | 沿球面下滑至某一点N,便离开球面做斜下抛运动 | |
| C. | 立即离开球面做平抛运动 | |
| D. | 以上说法都不正确 |
10. 如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
 如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )| A. | 2s末F做功的功率为0 | B. | 2s内小球的位移为20m | ||
| C. | 第1s内小球的速度变化了10m/s | D. | 第1s内F做功为100J |
17. 如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )
如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )
 如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )
如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )| A. | 人拉绳的力是200 N | |
| B. | 人拉绳的力是50 N | |
| C. | 人的脚给木板的摩擦力方向水平向左 | |
| D. | 人的脚给木板的摩擦力方向水平向右 |
18.关于空气湿度和热力学定律,下列说法正确的是 ( )
| A. | 热量可能会自发地从低温物体传向高温物体 | |
| B. | 功转变为热的实际宏观过程是可逆过程 | |
| C. | 空气的绝对湿度用空气中所含水蒸气的质量表示 | |
| D. | 无论、在冬季还是在夏季,当人们的皮肤感到干燥时,空气相对湿度一定较小 |

 如图所示,在光滑的水平面上有一质量为mA=0.5kg的木块A,现有质量为mB=0.1kg的小物块B以初速度v0=30m/s水平速度滑上A表面,由于B与A间有摩擦且A、B间的动摩擦因数为μ=0.2,B最终恰好在木块A的上表面右端边缘处相对A静止.求:
如图所示,在光滑的水平面上有一质量为mA=0.5kg的木块A,现有质量为mB=0.1kg的小物块B以初速度v0=30m/s水平速度滑上A表面,由于B与A间有摩擦且A、B间的动摩擦因数为μ=0.2,B最终恰好在木块A的上表面右端边缘处相对A静止.求: