题目内容
3.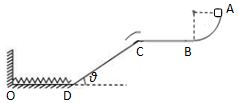 如图,质量为m=1kg的小滑块(视为质点)在半径为R=0.4m的$\frac{1}{4}$圆弧A端由静止开始释放,它运动到B点时速度为v=2m/s.当滑块经过B后立即将圆弧轨道撤去.滑块在光滑水平面上运动一段距离后,通过换向轨道由C点过渡到倾角为θ=37°、长s=1m的斜面CD上,CD之间铺了一层匀质特殊材料,其与滑块间的动摩擦系数可在0≤μ≤1.5之间调节.斜面底部D点与光滑地面平滑相连,地面上一根轻弹簧一端固定在O点,自然状态下另一端恰好在D点.认为滑块通过C和D前后速度大小不变,最大静摩擦力等于滑动摩擦力.取g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.
如图,质量为m=1kg的小滑块(视为质点)在半径为R=0.4m的$\frac{1}{4}$圆弧A端由静止开始释放,它运动到B点时速度为v=2m/s.当滑块经过B后立即将圆弧轨道撤去.滑块在光滑水平面上运动一段距离后,通过换向轨道由C点过渡到倾角为θ=37°、长s=1m的斜面CD上,CD之间铺了一层匀质特殊材料,其与滑块间的动摩擦系数可在0≤μ≤1.5之间调节.斜面底部D点与光滑地面平滑相连,地面上一根轻弹簧一端固定在O点,自然状态下另一端恰好在D点.认为滑块通过C和D前后速度大小不变,最大静摩擦力等于滑动摩擦力.取g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.(1)求滑块对B点的压力大小以及在AB上克服阻力所做的功;
(2)若设置μ=0,求质点从C运动到D的时间;
(3)若最终滑块停在D点,求μ的取值范围.
分析 (1)根据牛顿第二定律求出滑块在B点所受的支持力,从而得出滑块对B点的压力,根据动能定理求出AB端克服阻力做功的大小.
(2)若μ=0,根据牛顿第二定律求出加速度,结合位移时间公式求出C到D的时间.
(3)最终滑块停在D点有两种可能,一个是滑块恰好从C下滑到D,另一种是在斜面CD和水平面见多次反复运动,最终静止在D点,结合动能定理进行求解.
解答 解:(1)滑块在B点,受到重力和支持力,在B点,根据牛顿第二定律有:$F-mg=m\frac{{v}^{2}}{R}$,
代入数据解得:F=20N,
由牛顿第三定律得:F′=20N.
从A到B,由动能定理得:$mgR-W=\frac{1}{2}m{v}^{2}$,
代入数据得:W=2J.
(2)在CD间运动,有:mgsinθ=ma,
加速度为:a=gsinθ=10×0.6m/s2=6m/s2,
根据匀变速运动规律有:$s=vt+\frac{1}{2}a{t}^{2}$
代入数据解得:t=$\frac{1}{3}s$.
(3)最终滑块停在D点有两种可能:
a、滑块恰好能从C下滑到D.则有:
$mgsinθ•s-{μ_1}mgcosθ•s=0-\frac{1}{2}m{v^2}$,
代入数据得:μ1=1,
b、滑块在斜面CD和水平地面间多次反复运动,最终静止于D点.
当滑块恰好能返回C有:$-{μ}_{1}mgcosθ•2s=0-\frac{1}{2}m{v}^{2}$,
代入数据得到:μ1=0.125,
当滑块恰好能静止在斜面上,则有:mgsinθ=μ2mgcosθ,
代入数据得到:μ2=0.75.
所以,当0.125≤μ<0.75,滑块在CD和水平地面间多次反复运动,最终静止于D点.
综上所述,μ的取值范围是0.125≤μ<0.75或μ=1.
答:(1)滑块对B点的压力大小为20N,在AB上克服阻力所做的功为2J;
(2)质点从C运动到D的时间为$\frac{1}{3}s$;
(3)μ的取值范围为0.125≤μ<0.75或μ=1.
点评 解决本题的关键理清滑块在整个过程中的运动规律,运用动力学知识和动能定理进行求解,涉及到时间问题时,优先考虑动力学知识求解.对于第三问,要考虑滑块停在D点有两种可能.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案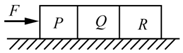 如图,水平地面上有三个靠在一起的物块P、Q和R,质量分别为m、2m和3m,物块与地面间的动摩擦因数都为μ.用水平恒力F推动物块P,一起向右匀加速运动,R和Q之间相互作用力大小F1,Q与P之间相互作用力大小F2,以下正确的是( )
如图,水平地面上有三个靠在一起的物块P、Q和R,质量分别为m、2m和3m,物块与地面间的动摩擦因数都为μ.用水平恒力F推动物块P,一起向右匀加速运动,R和Q之间相互作用力大小F1,Q与P之间相互作用力大小F2,以下正确的是( )| A. | 若μ≠0,F1=$\frac{1}{3}$F,F2=$\frac{5}{6}$F | B. | 若μ≠0,F1=$\frac{1}{2}$F,F2=$\frac{5}{6}$F | ||
| C. | 若μ=0,F1=$\frac{2}{3}$F,F2=$\frac{3}{4}$F | D. | 若μ=0,F1=$\frac{1}{2}$F,F2=$\frac{5}{6}$F |
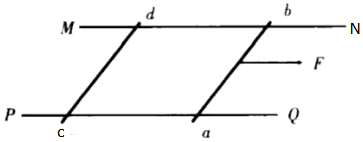
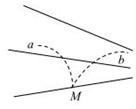 如图所示,实线为三条方向未知的电场线,从电场中的M点以相同的速度飞出a、b两个带电粒子,a、b的运动轨迹如图中虚线所示(不计a、b之间的库仑力及各自的重力),则( )
如图所示,实线为三条方向未知的电场线,从电场中的M点以相同的速度飞出a、b两个带电粒子,a、b的运动轨迹如图中虚线所示(不计a、b之间的库仑力及各自的重力),则( )| A. | a、b 一定带异种电荷 | |
| B. | 电场力对 a 做正功,对 b 做负功 | |
| C. | a 的速度将减小,b 的速度将增大 | |
| D. | a 的加速度将减小,b 的加速度将增大 |
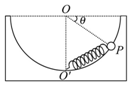 如图所示,质量为M、半径为R、内壁光滑的半球形容器静止放在粗糙水平地面上,O为球心,有一劲度系数为k的轻弹簧一端固定在半球底部O′处,另一端与质量为m的小球相连,小球静止于P点,已知地面与半球形容器间的动摩擦因数为μ,OP与水平方向的夹角为θ=30°,下列说法正确的是( )
如图所示,质量为M、半径为R、内壁光滑的半球形容器静止放在粗糙水平地面上,O为球心,有一劲度系数为k的轻弹簧一端固定在半球底部O′处,另一端与质量为m的小球相连,小球静止于P点,已知地面与半球形容器间的动摩擦因数为μ,OP与水平方向的夹角为θ=30°,下列说法正确的是( )| A. | 小球受到轻弹簧的弹力大小为$\frac{{\sqrt{3}}}{2}mg$ | |
| B. | 小球受到容器的支持力大小为mg | |
| C. | 小球受到容器的支持力大小为$\frac{1}{2}mg$ | |
| D. | 半球形容器受到地面的摩擦力大小为$\frac{{\sqrt{3}}}{2}mg$ |
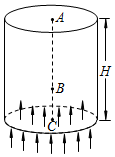 “娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比.人水平横躺时受风面积最大,此时人所受风力大于重力;站立时受风面积最小,此时人所受风力小于重力;如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.已知AB段距离大于BC段距离,关于表演者下落的过程,下列说法正确的是( )
“娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比.人水平横躺时受风面积最大,此时人所受风力大于重力;站立时受风面积最小,此时人所受风力小于重力;如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.已知AB段距离大于BC段距离,关于表演者下落的过程,下列说法正确的是( )| A. | 从A至B过程表演者的平均速度大于从B至C过程表演者的平均速度 | |
| B. | 从A至B过程表演者的运动时间等于从B至C过程表演者的运动时间 | |
| C. | 从A至B过程表演者加速度的绝对值大于从B至C过程表演者加速度的绝对值 | |
| D. | 从A至C的过程中,重力对表演者做的功等于表演者克服风力做的功 |
 等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )
等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )| A. | 试探电荷所受电场力的方向一直不变 | |
| B. | 试探电荷所受电场力的大小先减小后增大 | |
| C. | 试探电荷的电势能一直减小 | |
| D. | a、b、c三点电势为:φa<φb<φc |
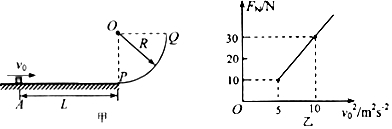
 如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )
如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )