题目内容
7. 某中学的排球训练场地为长18.0m,宽9.0m的长方形,场地中央的排球网高约为2.0m,训练中使用的排球质量为0.28kg,取g=10m/s2
某中学的排球训练场地为长18.0m,宽9.0m的长方形,场地中央的排球网高约为2.0m,训练中使用的排球质量为0.28kg,取g=10m/s2(1)若前排运动员跳起来在球网的上边缘沿垂直球网且水平的方向,将二传手传出的排球击中到对方场地的底线,不计排球被击出前的速度极其直径的大小,求运动运击球过程中对排球所做的功.
(2)站位在后排的运动员站在3m线处竖直向上起跳,并在最高点将球沿垂直球网方向水平击出后去,不计排球被击出前的速度极其直径的大小.
①若运动员跳起击球点的高度为2.5m,要想使排球既不触网也不出界,试分析说明击球的速度应满足什么条件
②若击球点的高度小于某个值,那么无论水平击球的速度多大,球不是触网就是出界,试求这个高度.
分析 (1)根据高度求出平抛运动的时间,结合水平位移求出初速度,从而得出击球过程中做功的大小.
(2)要想使排球既不触网也不出界,抓住两个临界情况,即恰好不触网,恰好不越界,结合平抛运动的规律求出初速度的范围.
(3)抓住临界情况,即球恰能擦网而过而不压对方底线边界,结合运动学公式求出高度的大小.
解答 解:(1)排球被击出后做平抛运动,运动的水平位移x=9.0m,下落的高度h=2.0m,
则平抛运动的时间$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×2}{10}}s=\sqrt{0.4}s$,
平抛运动的初速度${v}_{0}=\frac{x}{t}=\frac{9}{\sqrt{0.4}}m/s$,
击球过程中运动员对排球做功W=$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}×0.28×\frac{81}{0.4}J=28.35J$.
(2)①运动员将球水平击出后,球做平抛运动,设球刚好擦网而过,水平射程s1=3m,飞行时间${t}_{1}=\sqrt{\frac{2({h}_{2}-{h}_{1})}{g}}=\sqrt{\frac{2(2.5-2)}{10}}s=\frac{1}{\sqrt{10}}$s,
所以击球的最小速度为${v}_{1}=\frac{{s}_{1}}{{t}_{1}}=\frac{3}{\frac{1}{\sqrt{10}}}m/s=3\sqrt{10}m/s$,
设球恰好打在对方底线边界上,则水平射程s2=3m+9m=12m,此过程中球飞行的时间为
${t}_{2}=\sqrt{\frac{2{h}_{2}}{g}}=\sqrt{\frac{2×2.5}{10}}s=\frac{1}{\sqrt{2}}s$,
所以击球的最大速度${v}_{2}=\frac{{s}_{2}}{{t}_{2}}=\frac{12}{\frac{1}{\sqrt{2}}}m/s=12\sqrt{2}m/s$.
因此欲使球既不触网也不出界,则球的初速度满足$3\sqrt{10}m/s<{v}_{0}<12\sqrt{2}m/s$.
②设击球的高度为h2′时,球恰能擦网而过而不压对方底线边界,则对于球恰能擦网而过的情景有:
${v}_{1}=\frac{{s}_{1}}{{t}_{1}}=\frac{3}{\sqrt{\frac{2(h′-2)}{g}}}$,
而对于球恰能压对方底线边界的情景有:${v}_{2}=\frac{12}{\sqrt{\frac{2h′}{g}}}$,
若击出球的速度v<v1,则触网,若v>v2,则出界,所以必定存在v1=v2时球既不触网又能压对方底线边界有:v1=v2,即${{v}_{1}}^{2}={{v}_{2}}^{2}$,
联立上述三个方程可解得h′=2$\frac{2}{15}$m,即当$h′<2\frac{2}{15}m$时,无论击出球的速度v多大,球不是触网,就是出界.
答:(1)击球过程中对排球所做的功围为28.35J.
(2)欲使球既不触网也不出界,则球的初速度满足$3\sqrt{10}m/s<{v}_{0}<12\sqrt{2}m/s$.
当$h′<2\frac{2}{15}m$时,无论击出球的速度v多大,球不是触网,就是出界.
点评 本题考查平抛运动在生活中应用,要通过分析找出临界条件,由平抛运动的规律即可求解.

 由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )
由相关电磁学理论可以知道,若圆环形通电导线的中心为O,环的半径为R,环中通以电流为I,如图1所示,环心O处的磁感应强度大小B=$\frac{{μ}_{0}}{2}$$•\frac{I}{R}$,其中μ0为真空磁导率.若P点是过圆环形通电导线中心O点的轴线上的一点,且距O点的距离是x,如图2所示,有可能您不能直接求得P点处的磁感应强度B,但您能根据所学的物理知识判断出以下有关P点磁感应强度B的表达式是( )| A. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{2}I}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ | B. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{2}I}{({R}^{2}+{x}^{2})}$ | ||
| C. | BP=$\frac{{μ}_{0}}{2}$•$\frac{RI}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ | D. | BP=$\frac{{μ}_{0}}{2}$•$\frac{{R}^{3}I}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$ |
 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )| A. | 电流表的示数为4.4A | |
| B. | 原线圈的输入功率为16W | |
| C. | 电压表的示数为20V | |
| D. | 通过电阻R的交变电流的频率为100Hz |
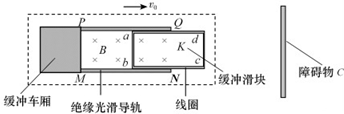
| A. | 线圈中的感应电流沿逆时针方向(俯视),最大感应电流为$\frac{BL{v}_{0}}{R}$ | |
| B. | 线圈对电磁铁的作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,线圈abcd产生的焦耳热为Q=$\frac{1}{2}$mv02 | |
| D. | 此过程中,通过线圈abcd的电荷量为q=$\frac{B{L}^{2}}{R}$ |
 如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )
如图,一根补课伸长的细线将一个小球悬挂于O点,用一直尺靠着线的左侧并沿着直线OA以速度v斜向上匀速运动,已知OA与水平方向的夹角θ=30°,则小球的速度( )| A. | 方向与水平方向的夹角为30°,大小为2v | |
| B. | 方向与水平方向的夹角为60°,大小为2v | |
| C. | 方向与水平方向的夹角为30°,大小为$\sqrt{3}$v | |
| D. | 方向与水平方向的夹角为60°,大小为$\sqrt{3}$v |
 如图所示,有一条沿顺时针方向匀速传递的水平传送带,恒定速度v=10m/s,传送带从左侧到右端长l=16m,将质量m=1kg的小物块放在其左端(小物块可视作质量),与此同时,给小物块沿传送带方向向的恒力F=6N,经过一段时间,小物块运动到其右端,已知物块与传送带之间的动摩擦因数μ=0.4,求物块从传送带左端到右端所需要的时间是多少?(g=10m/s2)
如图所示,有一条沿顺时针方向匀速传递的水平传送带,恒定速度v=10m/s,传送带从左侧到右端长l=16m,将质量m=1kg的小物块放在其左端(小物块可视作质量),与此同时,给小物块沿传送带方向向的恒力F=6N,经过一段时间,小物块运动到其右端,已知物块与传送带之间的动摩擦因数μ=0.4,求物块从传送带左端到右端所需要的时间是多少?(g=10m/s2) 如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.
如图所示,打点计时器固定在轨道上端,纸带穿过打点计时器与小车相连,平衡好摩擦力后接通电源,打点计时器工作,轻推小车使之匀速下滑(车轮不打滑),纸带上留下清晰的点迹.