题目内容
2.如图1,用一根长为L=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T.求(g=10m/s2,sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$,计算结果可用根式表示):
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
(3)细线的张力T与小球匀速转动的加速度ω有关,当ω的取值范围在0到ω′之间时,请通过计算求解T与ω2的关系,并在图2坐标纸上作出T-ω2的图象,标明关键点的坐标值.
分析 (1)小球刚要离开锥面时的速度,此时支持力为零,根据牛顿第二定律求出该临界角速度ω0.
(2)若细线与竖直方向的夹角为60°时,小球离开锥面,由重力和细线拉力的合力提供向心力,运用牛顿第二定律求解.
(3)根据小球的角速度较小,小球贴着锥面运动和离开锥面运动两个过程,分析并作出图象.
解答 解:(1)小球刚要离开锥面时的速度,此时支持力为零,根据牛顿第二定律得:
mgtanθ=mω${{ω}_{0}}^{2}$Lsin θ
解得:ω0=$\sqrt{\frac{g}{Lcosθ}}=\sqrt{12.5}$rad/s.
(2)同理,当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式有:
mgtan α=mω′2Lsin α
解得:ω′=$\sqrt{\frac{g}{Lcosα}}=2\sqrt{5}$rad/s.
(3)a.当ω1=0时 T1=mgcosθ=8N,标出第一个特殊点坐标( 0,8N);
b.当0<ω<$\sqrt{12.5}$rad/s时,根据牛顿第二定律得:
Tsinθ-Ncosθ=mω2Lsinθ,
Tcosθ+Nsinθ=mg
解得$T=mgcosθ+mL{ω}^{2}(sinθ)^{2}=8+\frac{9}{25}{ω}^{2}$
当${ω}_{2}=\sqrt{12.5}rad/s$时,T2=12.5N 标出第二个特殊点坐标[12.5(rad/s)2,12.5N];
c.当$\sqrt{12.5}rad/s≤ω≤2\sqrt{5}rad/s$时,小球离开锥面,设细线与竖直方向夹角为β,
${T}_{3}sinβ=m{ω}^{2}Lsinβ$
解得:${T}_{3}=mL{ω}^{2}$
当$ω=ω′=2\sqrt{5}rad/s$时,T3=20N
标出第三个特殊点坐标[20(rad/s)2,20N].
画出T-ω2图象如图所示.
答:
(1)若要小球离开锥面,则小球的角速度ω0至少为$\sqrt{12.5}$rad/s.
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为2$\sqrt{5}$rad/s.
(3)T-ω2的图象如上所示.
点评 本题的关键点在于判断小球是否离开圆锥体表面,不能直接应用向心力公式求解,并要运用数学知识作出图象,难度较大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 地球绕太阳运行的周期T地及地日中心间的距离r日地 | |
| B. | 月球绕地球运行的周期T月及地日中心间的距离r月地 | |
| C. | 人造地球卫星在地面附近绕行时的运行周期T | |
| D. | 若不考虑地球的自转,已知地球的半径R和地球表面的重力加速度g |
| A. | 匀速圆周运动是速度大小不变的匀变速曲线运动 | |
| B. | 开普勒利用扭称实验了万有引力常量的数值 | |
| C. | 行星绕恒星运动轨道为圆形,则它运动的周期平方与轨道半径的三次方之比$\frac{{T}^{2}}{{R}^{3}}$=K为常数,此常数的大小与恒星的质量和行星的速度有关 | |
| D. | 牛顿发现了万有引力定律 |
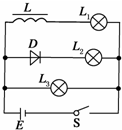 如图所示的电路中,三个灯泡L1、L2、L3的电阻关系为R1<R2<R3,电感L的电阻可忽略,D为理想二极管.电键S从闭合状态突然断开时,则下列判断正确的是( )
如图所示的电路中,三个灯泡L1、L2、L3的电阻关系为R1<R2<R3,电感L的电阻可忽略,D为理想二极管.电键S从闭合状态突然断开时,则下列判断正确的是( )| A. | L1立即熄灭 | B. | L2先变亮,然后熄灭 | ||
| C. | L3先变亮,然后熄灭 | D. | L2立即熄灭 |
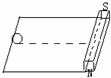 如图,一光滑的平面上,右方有一条形磁铁,一金属环以初速度V沿磁铁的中线向右滚动,则以下说法正确的是( )
如图,一光滑的平面上,右方有一条形磁铁,一金属环以初速度V沿磁铁的中线向右滚动,则以下说法正确的是( )| A. | 环的速度越来越小 | B. | 环保持匀速运动 | ||
| C. | 环的速度越来越大 | D. | 环的速度先增大后减小 |
| A. | 10-13N | B. | 10-9N | C. | 10-5 N | D. | 10-1N |
| A. | 若v=0.5c,火箭上的观察者测得火箭的长度仍为30m | |
| B. | 若v=0.5c,地面上的观察者测得火箭的长度仍为30m | |
| C. | 若v=0.5c,火箭上的观察者认为地面上的时钟走得快 | |
| D. | 若v=0.5c,地面上的观察者认为火箭上的时钟走得慢 | |
| E. | 若v?0.5c,地面上和火箭上的观察者测得火箭的长度相同 |

 随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动,设飞船中具有基本测量工具.
随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动,设飞船中具有基本测量工具.