题目内容
6. 如图所示,半径R=0.4m的光滑半圆形管道(管道内径远小于R)竖直固定在水平面上,管道最低点B与粗糙水平面相切,理想弹簧发射器固定于水平面上,发射器管口在A处.某次实验中,发射器将质量m=0.1kg的小物块(可视为质点)弹出,小物块沿圆管道恰好到达最高点C.已知小物块与水平面间的动摩擦因数μ=0.2,A、B间距L=1m,且A、B、C在同一竖直面.求:
如图所示,半径R=0.4m的光滑半圆形管道(管道内径远小于R)竖直固定在水平面上,管道最低点B与粗糙水平面相切,理想弹簧发射器固定于水平面上,发射器管口在A处.某次实验中,发射器将质量m=0.1kg的小物块(可视为质点)弹出,小物块沿圆管道恰好到达最高点C.已知小物块与水平面间的动摩擦因数μ=0.2,A、B间距L=1m,且A、B、C在同一竖直面.求:(1)小物块到达B点时的速度vB和小物块在管道最低点B处受到的支持力大小;
(2)在AB段摩擦力对小物块所做功的大小;
(3)小物块离开发射器管口时的动能.
分析 (1)抓住小物块恰好到达C点,得出C点的速度,结合机械能守恒求出B点的速度,根据牛顿第二定律求出支持力.
(2)根据功的公式求出AB段摩擦力做功的大小.
(3)对A到B过程运用动能定理,求出小物块离开发射器管口时的动能.
解答 解:(1)小物块恰到C点,则vC=0,
从B点到C点,小物块机械能守恒,有:$\frac{1}{2}m{{v}_{B}}^{2}=mg•2R$,
代入数据解得${v}_{B}=\sqrt{4gR}=\sqrt{4×10×0.4}$m/s=4m/s.
B处,由牛顿第二定律得:${F}_{N}-mg=m\frac{{{v}_{B}}^{2}}{R}$,
代入数据解得FN=5N.
(2)摩擦力对小物块所做的功 Wf=-μmgL=-0.2×1×1J=-0.2J.
(3)对A到B过程,运用动能定理得:Wf=$\frac{1}{2}$mv2B-EKA,
代入数据解得EKA=1J.
答:(1)小物块到达B点时的速度为4m/s,小物块在管道最低点B处受到的支持力大小为5N.
(2)在AB段摩擦力对小物块所做功的大小为-0.2J;
(3)小物块离开发射器管口时的动能为1J.
点评 本题考查了动能定理和圆周运动的基本运用,知道圆周运动向心力的来源,以及最高点的临界情况是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
9.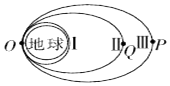 发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )
发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )
 发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )
发射月球探测卫星要经过多次变轨.如图所示,I是某月球探测卫旱发射后的近地圆轨道.II、III是两次变轨后的转移椭圆轨道,O点是II、III轨道的近地点,Q、P分别是II、III轨道的远地点.则下列说法止确的是( )| A. | 在二个轨道上,卫星在O点的速度相同 | |
| B. | 在三个轨道上,卫星在O点的加速度相同 | |
| C. | 卫星在Q点的机械能大于其在P点的机械能 | |
| D. | 卫星在Q点的机械能小于其在P点的机械能 |
10.一质量为m的物体以一定的速度水平抛出,不计空气阻力,重力加速度为g,下面说法中正确的是( )
| A. | 在刚抛出物体的瞬间,动量的变化率为0 | |
| B. | 在任何时间内,动量的变化率为mg | |
| C. | 在任何时间内,动量变化的方向都是竖直向下 | |
| D. | 在相等的时间间隔内,动量的变化量逐渐变大 |
7.起重机用4s的时间把重为2×104 N的货物匀速提升10m,则该起重机对货物做功的功率为( )
| A. | 2×103 W | B. | 8×102 W | C. | 5×104 W | D. | 8×104 W |
18. 如图所示,某质点做匀减速直线运动,依次经过A、B、C三点,最后停在D点.已知AB=6m,BC=4m,从A点运动到B点,从B点运动到C点两个过程速度变化量都为-2m/s,则下列说法正确的是( )
如图所示,某质点做匀减速直线运动,依次经过A、B、C三点,最后停在D点.已知AB=6m,BC=4m,从A点运动到B点,从B点运动到C点两个过程速度变化量都为-2m/s,则下列说法正确的是( )
 如图所示,某质点做匀减速直线运动,依次经过A、B、C三点,最后停在D点.已知AB=6m,BC=4m,从A点运动到B点,从B点运动到C点两个过程速度变化量都为-2m/s,则下列说法正确的是( )
如图所示,某质点做匀减速直线运动,依次经过A、B、C三点,最后停在D点.已知AB=6m,BC=4m,从A点运动到B点,从B点运动到C点两个过程速度变化量都为-2m/s,则下列说法正确的是( )| A. | 质点到达B点时速度大小为2.55 m/s | |
| B. | 质点的加速度大小为2 m/s2 | |
| C. | 质点从A点运动到C点的时间为4 s | |
| D. | A、D两点间的距离为10.25 m |
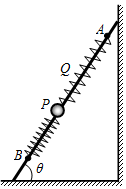 如图,固定直杆上套有一小球和两根轻弹簧,两根轻弹簧的一端与小球相连,另一端分别固定在杆上相距为2L的A、B两点.直杆与水平面的夹角为θ,小球质量为m,两根轻弹簧的原长均为L、劲度系数均为$\frac{3mgsinθ}{L}$,g为重力加速度.
如图,固定直杆上套有一小球和两根轻弹簧,两根轻弹簧的一端与小球相连,另一端分别固定在杆上相距为2L的A、B两点.直杆与水平面的夹角为θ,小球质量为m,两根轻弹簧的原长均为L、劲度系数均为$\frac{3mgsinθ}{L}$,g为重力加速度. 如图所示,传送带与水平方向的夹角θ=37°,上端与一段斜面BC相连,斜面BC的倾角也为θ,半径为R的光滑圆弧轨道CD与斜面BC相切于C,圆弧轨道的最高点D,圆心O与B点在同一竖直线上,传送带AB的长度为L=2R,始终沿顺时针方向转动,一质量为m的小滑块以初速度v0=$\sqrt{8.8gR}$(g为重力加速度)从A点冲上传送带,小滑块与传送带及斜面间的动摩擦因数均为μ=0.25,取sin37°=0.6,cos37°=0.8,求:
如图所示,传送带与水平方向的夹角θ=37°,上端与一段斜面BC相连,斜面BC的倾角也为θ,半径为R的光滑圆弧轨道CD与斜面BC相切于C,圆弧轨道的最高点D,圆心O与B点在同一竖直线上,传送带AB的长度为L=2R,始终沿顺时针方向转动,一质量为m的小滑块以初速度v0=$\sqrt{8.8gR}$(g为重力加速度)从A点冲上传送带,小滑块与传送带及斜面间的动摩擦因数均为μ=0.25,取sin37°=0.6,cos37°=0.8,求: 如图甲所示,发动机用一根轻绳跨过定滑轮,由静止开始沿着光滑的斜面拉升一物体,斜面的倾角为θ=30°;该过程中,牵引力和物体速度倒数的关系图象如图乙,物体速度和时间的关系图象如图丙,图象中F0,vm、△t为已知量(△t为物体做变加速运动的时间),不计一切摩擦,重力加速度为g,求:
如图甲所示,发动机用一根轻绳跨过定滑轮,由静止开始沿着光滑的斜面拉升一物体,斜面的倾角为θ=30°;该过程中,牵引力和物体速度倒数的关系图象如图乙,物体速度和时间的关系图象如图丙,图象中F0,vm、△t为已知量(△t为物体做变加速运动的时间),不计一切摩擦,重力加速度为g,求: 如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.