题目内容
15.如图所示,一个人用与水平方向成θ=30°角斜向下的推力F推一个重为G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.40.求:(1)推力F的大小;
(2)若人不改变推力F的大小,只把力的方向变为水平,去推这个静止的箱子,且当作用的时间t=3s后撤去推力,则撤去推力后箱子还能运动多长时间?

分析 (1)对箱子受力分析,抓住竖直方向和水平方向合力为零求出推力F的大小.
(2)根据牛顿第二定律求出箱子的加速度;根据速度时间公式求出3s末的速度,结合牛顿第二定律求出撤去推力后的加速度,结合速度时间公式求出箱子还能滑行的时间.
解答 解:(1)物体受重力、推力、支持力和摩擦力处于平衡,有:
Fcos30°=f,
Fsin30°+mg=N,
f=μN,
代入数据联立解得:F≈120N.
(2)根据牛顿第二定律得,箱子的加速度为:
a=$\frac{F-μmg}{m}=\frac{120-0.40×200}{20}=2m/{s}^{2}$,
3s后的速度为:v=at=2×3m/s=6m/s.
撤去推力后的加速度为:$a′=\frac{μmg}{m}=μg=0.40×10=4\\;m/{s}^{2}$m/s2,
则箱子还能滑行的时间为:$t′=\frac{v}{a′}=\frac{6}{4}s=1.5s$.
答:(1)推力F的大小为120N.
(2)箱子还能滑行的时间为1.5s.
点评 本题考查了共点力的平衡、牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
5.气球吊着物体匀速下降到某一高度时.绳子突然断了,则在绳断的瞬间物体将具有 (不计空气阻力)( )
| A. | 重力加速度为g,没有速度 | B. | 向下的速度,而加速度为零 | ||
| C. | 向下的速度和向下的加速度 | D. | 物体将做自由落体运动 |
6.质量m=1kg的物体在光滑水平面上运动,初始时速度V0大小为2m/s,在物体运动的直线上施以一水平恒力,经过t=1s,速度大小变为4m/s,则这个力的大小可能是( )
| A. | 1N | B. | 2N | C. | 6N | D. | 7N |
10. 某同学在探究摩擦力的实验中采用了如图所示的操作,将一个长方体木块放在水平桌面上,然后用一个力传感器对木块施加一个水平拉力F,并用另外一个传感器对木块的运动状态进行监测,如表是她记录的实验数据.木块的重力为10.00N,重力加速度g=9.80m/s2,根据表格中的数据回答下列问题(答案要求有3位有效数字):
某同学在探究摩擦力的实验中采用了如图所示的操作,将一个长方体木块放在水平桌面上,然后用一个力传感器对木块施加一个水平拉力F,并用另外一个传感器对木块的运动状态进行监测,如表是她记录的实验数据.木块的重力为10.00N,重力加速度g=9.80m/s2,根据表格中的数据回答下列问题(答案要求有3位有效数字):
(1)木块与桌面间的最大静摩擦力Ffm>4.01N;
(2)木块与桌面间的动摩擦因数μ=0.401;
(3)实验次数5中监测到的加速度a=1.45m/s2.
 某同学在探究摩擦力的实验中采用了如图所示的操作,将一个长方体木块放在水平桌面上,然后用一个力传感器对木块施加一个水平拉力F,并用另外一个传感器对木块的运动状态进行监测,如表是她记录的实验数据.木块的重力为10.00N,重力加速度g=9.80m/s2,根据表格中的数据回答下列问题(答案要求有3位有效数字):
某同学在探究摩擦力的实验中采用了如图所示的操作,将一个长方体木块放在水平桌面上,然后用一个力传感器对木块施加一个水平拉力F,并用另外一个传感器对木块的运动状态进行监测,如表是她记录的实验数据.木块的重力为10.00N,重力加速度g=9.80m/s2,根据表格中的数据回答下列问题(答案要求有3位有效数字):| 实验次数 | 运动状态 | 水平拉力F/N |
| 1 | 静止 | 3.62 |
| 2 | 静止 | 4.00 |
| 3 | 匀速 | 4.01 |
| 4 | 匀加速 | 5.01 |
| 5 | 匀加速 | 5.49 |
(2)木块与桌面间的动摩擦因数μ=0.401;
(3)实验次数5中监测到的加速度a=1.45m/s2.
7.如图,当正电荷从A到C移动过程中,加速度为a,则正确的是( )


| A. | EA<EB | B. | aA<aB | C. | 电势φA>φB | D. | 电势能可能增加 |
4. 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )| A. | 减小狭缝间的距离 | B. | 增大磁场的磁感应强度 | ||
| C. | 增大D形金属盒的半径 | D. | 增大匀强电场间的加速电压 |
5.下面为四个质点的图象,其中反映质点做匀加速直线运动的是( )
| A. |  | B. |  | C. |  | D. |  |
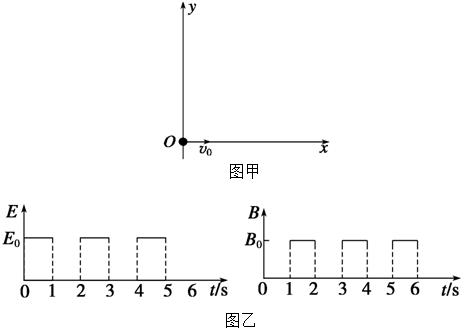 如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求: