题目内容
16. 如图所示,半径为$\frac{1}{4}$l、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l.当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内).求:计算结果可以带根号,g不要带具体值.
如图所示,半径为$\frac{1}{4}$l、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l.当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内).求:计算结果可以带根号,g不要带具体值.(1)竖直杆角速度ω为多大时,小球恰离开竖直杆.
(2)ω至少达到多少时b轻绳伸直开始有拉力.
分析 (1)小球恰离开竖直杆时,受重力和拉力,拉力的竖直分力与重力平衡,水平分力提供向心力;
(2)角速度ω再增大,轻绳b拉直后,小球做圆周运动的半径为r=lsin60°的匀速圆周运动,再根据拉力的竖直分力与重力平衡,水平分力提供向心力列式求解.
解答 解:(1)小球恰离开竖直杆时,小球与竖直杆间的作用力为零,此时轻绳a与竖直杆间的夹角为α,由题意可知sinα=$\frac{1}{4}$,r=$\frac{l}{4}$,
沿半径:Fasinα=mω2r
垂直半径:Facosα=mg
联立解得ω=$2\sqrt{\frac{g}{\sqrt{15}l}}$
(2)角速度ω再增大,轻绳b拉直后,小球做圆周运动的半径为r=lsin60°
沿半径:Fasin60°=mω2r
垂直半径:Facos60°=mg
联立解得ω2≥$\sqrt{\frac{2g}{l}}$
答:(1)竖直杆角速度ω为$2\sqrt{\frac{g}{\sqrt{15}l}}$时,小球恰离开竖直杆;
(2)ω至少达到$\sqrt{\frac{2g}{l}}$时b轻绳伸直开始有拉力.
点评 本题关键是明确明确小球合力的水平分力提供向心力,竖直分力平衡,要求同学们能正确分析小球的受力情况,难度适中.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6.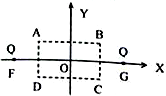 如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
 如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )| A. | O点电势最高 | |
| B. | A、C两点电场强度相同 | |
| C. | B、D两点电势相等 | |
| D. | 若将点电荷-q从A点移向C,电势能减小 |
7. 如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
 如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )| A. | 人对绳子的拉力保持不变 | B. | 人拉的绳子端点匀速下降 | ||
| C. | 人拉的绳子端点加速下降 | D. | 人对绳子做功的功率保持不变 |
11.物体做初速度为零的匀加速直线运动,第5s内的位移是18m,则以下结论正确的是( )
| A. | 物体的加速度是3.6m/s2 | B. | 物体的加速度是4m/s2 | ||
| C. | 物体在第4s内的位移是16m | D. | 物体在5s内的位移是50m |
8.2015年10月7日12时13分,我国在酒泉卫星发射中心用长征二号运载火箭成功将1组“吉林一号”商业卫星(1颗光学遥感卫星、2颗视频卫星和1颗技术验证卫星)发射升空,其工作轨道均高约650公里.“吉林一号”卫星的发射成功是一个里程碑,它创造性地采用“星载一体化”设计,标志着我国航天遥感应用领域商业化、产业化发展迈出重要一步,下列说法正确的是( )
| A. | “吉林一号”卫星环绕地球运动的速度大于第一宇宙速度 | |
| B. | 根据题中数据可以估测地球的质量 | |
| C. | “吉林一号”卫星的轨道有可能在地球极地附近通过 | |
| D. | “吉林一号”卫星的周期大于同步地球卫星的周期 |
17. 如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
 如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )| A. | A、B、C三者的加速度相同 | B. | 三者中A、C将同时滑到斜面底端 | ||
| C. | 滑到斜面底端时,B的速度最大 | D. | 三者的位移大小相同 |
18.有甲、乙、丙、丁四位同学在做“研究气体实验定律实验”,分别得到如下四幅图象(如图所示).则如下的有关他们的说法,不正确的是( )


| A. | 若甲研究的是查理定律,则他作的图象可能是图a | |
| B. | 若乙研究的是玻意耳定律,则他作的图象是图b | |
| C. | 若丙研究的是查理定律,则他作的图象可能是图c | |
| D. | 若丁研究的是盖-吕萨克定律,则他作的图象是图d |
 有一小船正在渡河,如图所示,在到达离对岸30m的P点时,其下游40m处有一危险水域,船的发动机可以使船在静水中以6m/s的速度行驶,假若水流速度为5m/s,求:
有一小船正在渡河,如图所示,在到达离对岸30m的P点时,其下游40m处有一危险水域,船的发动机可以使船在静水中以6m/s的速度行驶,假若水流速度为5m/s,求: 在2015短道速滑世锦赛女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,为提高速滑成绩,选手在如下场地进行训练:赛道的直道长度为L=30m,弯道半径为R=2.5m,忽略冰面对选手的摩擦力,且冰面对人的弹力沿身体方向,在过弯道时,身体与冰面的夹角θ为45°,直线加速过程视为匀加速过程,加速度a=1m/s2,若训练过程中选手没有减速过程,为保证速滑不出现意外情况,选手在直道上加速的最短时间为多少?(g取10m/s2)
在2015短道速滑世锦赛女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,为提高速滑成绩,选手在如下场地进行训练:赛道的直道长度为L=30m,弯道半径为R=2.5m,忽略冰面对选手的摩擦力,且冰面对人的弹力沿身体方向,在过弯道时,身体与冰面的夹角θ为45°,直线加速过程视为匀加速过程,加速度a=1m/s2,若训练过程中选手没有减速过程,为保证速滑不出现意外情况,选手在直道上加速的最短时间为多少?(g取10m/s2)