题目内容

2．如图，物体在斜面上保持静止状态，下列说法正确的是（　　）
A．重力可分解为沿斜面向下的力和对斜面的压力
B．物体对斜面的压力与斜面对物体的支持力是一对作用力与反作用力
C．重力沿斜面向下的分力与斜面对物体的摩擦力是一对平衡力
D．斜面对物体的作用力一定竖直向上

分析 物体在斜面上保持静止状态，其重力可分解为沿斜面向下的分力和垂直于斜面向下的分力，不能说成压力．压力的受力体是斜面．而重力分力的受力体是物体．物体受到重力、斜面的支持力和静摩擦力，根据平衡条件可知重力沿斜面向下的分力与斜面对物体的静摩擦力是平衡力．物体对斜面的压力与斜面对物体的支持力是一对作用力与反作用力，不是平衡力．重力垂直于斜面方向的分力与斜面对物体的支持力是平衡力．

解答 解：A、重力可分解为沿斜面向下的分力和垂直于斜面向下的分力，不能说成对斜面的压力．故A错误．
B、物体和斜面之间由于相互挤压而使物体受到了斜面的支持力，而斜面受到了物体的压力，二力是一对相互作用力．故B正确．
C、物体受到重力、斜面的支持力和静摩擦力，根据平衡条件可知重力沿斜面向下的分力与斜面对物体的静摩擦力是平衡力，故C正确；
D、物体处于平衡状态，则物体受到的合外力等于0，其中物体受到的斜面的支持力与摩擦力的和一定与物体受到的重力平衡，所以物体受到的斜面的支持力与摩擦力的和大小与重力相等，方向竖直向上．故D正确
故选：BCD

点评 本题考查的均为易错点，要求我们在学习中应注意准确地掌握相关概念和规律，不能似是而非，否则在解题时极易出错．

练习册系列答案
相关题目
6．下列说法中正确的是（　　）
A．两个匀速直线运动的合运动，可能是曲线运动
B．两个匀变速直线运动的合运动，可能是直线运动
C．一个匀速直线和匀变速直线运动的合运动，可能是匀速直线运动
D．一个匀速直线和匀变速直线运动的合运动，一定是曲线运动
13．如图所示的电路中，电灯A和B与固定电阻的阻值均为R，L是自感系数较大的线圈．当S1闭合、S2断开且电路稳定时，AB亮度相同，再闭合S2，待电路稳定后将S1断开时，下列说法正确的是（　　）
A．B灯立即熄灭B．A灯将比原来更亮一些后再熄灭
C．有电流通过B灯，方向为c→B→dD．有电流通过A灯，方向为b→A→a
10．水平地面A点正上方不同高度处有两个完全相同的小球a、b，现将两球沿水平方向同时水平抛出，两球运动轨迹相交于B点，空气阻力不计，则（　　）
A．两球可能相遇B．两球初速度可能相同
C．经过B点时两球速度方向可能相同D．经过B点时两球速度大小可能相等
17．如图所示，用细绳系一小球，使小球在水平面内做匀速圆周运动，不计空气阻力，关于小球的受力正确的是（　　）
A．只受重力B．只受绳子拉力
C．受重力、绳子拉力D．受重力、绳子拉力和向心力
7．如图甲所示，在利用重物自由下落验证机械能守恒定律的实验中，某实验小组打出了三条纸带，但是由于实验操作不规范，三条打点纸带的第1个点和第2个点之间的距离都明显的大于2mm，于是他们选择了如图乙所示的一条点迹清晰且在一条直线上的纸带进行数据处理．他们首先在所选择纸带的前四个点的下方标上1、2、3、4，在后面适当位置又选了五个计数点A、B、C、D、E；然后，他们又设计了四种数据处理方案来验证机械能守恒定律．
方案1：选择第1个点作为过程的起点，分别选择计数点B、C、D作为过程的终点，用刻度尺量出计数点A、B、C、D、E到第1个点的距离h1、h2、h3、h4、h5，再数出计数点B、C、D到第1个点的时间间隔数k，利用Vn=gkT算出重物运动到计数点B、C、D时的速度，比较“mghn和$\frac{1}{2}$m${V}_{n}^{2}$”是否相等来验证机械能是否守恒．
方案2：选择第1个点作为过程的起点，分别选择计数点B、C、D作为过程的终点，用刻度尺量出计数点A、B、C、D、E到第1个点的距离h1、h2、h3、h4、h5，利用Vn=$\frac{{{h}_{n+1}-h}_{n-1}}{2T}$算出重物运动到计数点B、C、D时的速度，比较“mghn和$\frac{1}{2}$m${V}_{n}^{2}$”是否相等来验证机械能是否守恒．
方案3：选择第3个点作为过程的起点，分别选择计数点B、C、D作为过程的终点，用刻度尺量出计数点A、B、C、D、E到第3个点的距离h1、h2、h3、h4、h5，再数出计数点B、C、D到第1个点的时间间隔数k，利用Vn=gkT算出重物运动到计数点B、C、D时的速度，利用V3=2gT求出打第3个点时重物的速度，比较“mghn和（$\frac{1}{2}$m${V}_{n}^{2}$-$\frac{1}{2}$m${V}_{3}^{2}$）”是否相等来验证机械能是否守恒．
方案4：选择第3个点作为过程的起点，分别选择计数点B、C、D作为过程的终点，用刻度尺量出计数点A、B、C、D、E到第3个点的距离h1、h2、h3、h4、h5，利用Vn=$\frac{{{h}_{n+1}-h}_{n-1}}{2T}$算出重物运动到计数点B、C、D时的速度，再测出第2个点到第4个点之间的距离S，利用V3=$\frac{S}{2T}$求出打第3个点时重物的速度，比较“mghn和（$\frac{1}{2}$m${V}_{n}^{2}$-$\frac{1}{2}$m${V}_{3}^{2}$）”是否相等来验证机械能是否守恒．

（1）你认为最合适的方案是方案4．
（2）说出两条你认为其他方案不合适的理由：
理由1：研究过程的起点不能选在第1点．
理由2：不能用v=gt计算速度．
14．在“验证机械能守恒定律”的实验中，重物自由下落，纸带上打出一系列的点，如图所示，相邻计数点间的时间间隔为0.02s．
（1）打点计时器打下计数点B时，重物下落的速度vB=0.978m/s；（计算结果保留三位有效数字）
（2）经过多次测量及计算发现，重物重力势能的减小量△Ep略大于动能的增加量△Ek，这是由于纸带与打点计时器之间存在摩擦等原因造成的，由此得出结论：在实验误差允许范围内，机械能守恒．
11．从大型加速器射出的电子束总能量约为500GeV（1GeV=1.6×10-10J），此能量最接近（　　）
A．一只爬行的蜗牛的动能B．一个奔跑的孩子的动能
C．一辆行驶的轿车的动能D．一架飞行的客机的动能
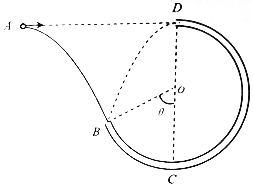17．如图所示，一个可视为质点的质量为m=1kg的小球，以某一初速度从A点水平抛出，恰好从竖直圆管BCD的B点沿切线方向进入圆管，经BCD后从圆管的最高点D水平射出，恰好又落到B点．已知圆弧的半径为R=0.3m，且A与D在同一水平线上，BC弧对应的圆心角θ=60°，不计空气阻力，g=10m/s2．求：
（1）AB两点间的水平距离；
（2）小球第一次落在B点时，小球对管壁的做用力大小；
（3）试判断圆弧管道是否光滑，并简要说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网