题目内容
17. 如图所示在水平地面O处固定一竖直挡板OM段光滑,M点右侧粗糙,质量为m,带电量为+q的粗糙物块a恰能静止于M点,有一质量为2m,带电量也为+q的光滑物块b以初速度v0=$\sqrt{\frac{gL}{2}}$从N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连.每次ab与档板碰撞后均原速率弹回,整个装置牌水平向左的匀强电场中,且电场强度E=$\frac{mg}{2q}$.物块a,b均视为质点,且滑块受的最大静摩擦力等于滑动摩擦力,求:
如图所示在水平地面O处固定一竖直挡板OM段光滑,M点右侧粗糙,质量为m,带电量为+q的粗糙物块a恰能静止于M点,有一质量为2m,带电量也为+q的光滑物块b以初速度v0=$\sqrt{\frac{gL}{2}}$从N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连.每次ab与档板碰撞后均原速率弹回,整个装置牌水平向左的匀强电场中,且电场强度E=$\frac{mg}{2q}$.物块a,b均视为质点,且滑块受的最大静摩擦力等于滑动摩擦力,求:(1)a,b第一次碰撞后紧靠在一起的初速度vAB
(2)a,b第一次向右经过M点后两者之间的最大距离△s
(3)系统由于摩擦和碰撞所产生的总内能E内.
分析 (1)根据动能定理求出b与a碰撞前的速度,再根据动量守恒定律求出a、b第一次碰撞后紧靠在一起的初速度.
(2)a、b在MO之间运动过程中只有电场力做功,故a、b返回M点时速度仍为vAB,且来到M 点后由于A受到摩擦力和电场力作用,造成ab分离.a速度减为零后,电场力和摩擦力平衡,处于静止,b速度继续减小,当b速度减为零时,两者的距离最大.
(3)物块a、b最终紧靠一起在OM间作往复运动,由能的转化和守恒定律求出产生的总内能.
解答 解:(1)对b运动动能定理得,有:$qEL=\frac{1}{2}2m{{v}_{1}}^{2}$-$\frac{1}{2}2m{{v}_{0}}^{2}$,
解得v1=$\sqrt{gL}$,
根据动量守恒定律得,2mv1=3mvAB,
解得${v}_{AB}=\frac{2}{3}\sqrt{gL}$.
(2)a、b返回M点时速度仍为vAB,经过到M 点后由于a受到摩擦力和电场力作用,b受到电场力作用,两者分离.
因为开始带电量为+q的粗糙物块a恰能静止于M点,则有qE=f=$\frac{mg}{2}$,
对a,加速度大小${a}_{1}=\frac{qE+f}{m}=g$,对b,加速度大小${a}_{2}=\frac{qE}{m}=\frac{1}{2}g$,
当a速度减为零后,a处于静止,可知b的速度减为零时,两者的距离最大.
$△s=\frac{{{v}_{AB}}^{2}}{2{a}_{2}}-\frac{{{v}_{AB}}^{2}}{2{a}_{1}}$=$\frac{2}{9}L$.
(3)物块a、b最终紧靠一起在OM间作往复运动,由能的转化和守恒定律有:E内=$\frac{1}{2}2m{{v}_{0}}^{2}+qEL$=mgL.
答:(1)a、b第一次碰撞后紧靠在一起的初速度为$\frac{2}{3}\sqrt{gL}$;
(2)a,b第一次向右经过M点后两者之间的最大距离△s为$\frac{2}{9}L$;
(3)系统由于摩擦和碰撞所产生的总内能E内为mgL.
点评 本题综合考查了动能定理、动量守恒定律和能量守恒定律,综合性强,对学生能力要求高,关键是理清运动过程,确定出最终的运动状态,运用合适的规律进行求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,金属导轨上的导体棒ab与导轨垂直且接触良好,整个装置位于竖直平面内,并处在垂直轨道平面向外的匀强磁场中.在与金属轨道相连接的带有铁芯的线圈的左侧,悬挂着一个闭合线圈c.要使线圈c中产生感应电流,导体棒ab应在导轨上做下列哪种运动( )
如图所示,金属导轨上的导体棒ab与导轨垂直且接触良好,整个装置位于竖直平面内,并处在垂直轨道平面向外的匀强磁场中.在与金属轨道相连接的带有铁芯的线圈的左侧,悬挂着一个闭合线圈c.要使线圈c中产生感应电流,导体棒ab应在导轨上做下列哪种运动( )| A. | 向右做匀速运动 | B. | 向左做匀速运动 | C. | 向右做减速运动 | D. | 向右做加速运动 |
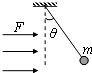 在科学研究中,可以用风力仪直接测量风力的大小,其原理如图所示.仪器中有一根轻质金属丝,悬挂着一个金属球,无风时,金属丝竖直下垂;当有沿水平方向吹来的风时,金属丝偏离竖直方向一个角度,风力越大,偏角越大.那么,风力的大小F和小球质量m、偏角θ的关系是( )
在科学研究中,可以用风力仪直接测量风力的大小,其原理如图所示.仪器中有一根轻质金属丝,悬挂着一个金属球,无风时,金属丝竖直下垂;当有沿水平方向吹来的风时,金属丝偏离竖直方向一个角度,风力越大,偏角越大.那么,风力的大小F和小球质量m、偏角θ的关系是( )| A. | F=mgsinθ | B. | F=$\frac{mg}{cosθ}$ | C. | F=mgtanθ | D. | F=$\frac{mg}{tanθ}$ |
 如图所示 一固定光滑斜面上有A、B两个物体,已知A的质量为mA,B的质量为mB,现两物体紧挨着一起沿斜面下滑,则A、B间的作用力是( )
如图所示 一固定光滑斜面上有A、B两个物体,已知A的质量为mA,B的质量为mB,现两物体紧挨着一起沿斜面下滑,则A、B间的作用力是( )| A. | mAgsinα | B. | mBgsinα | C. | 0 | D. | (mA+mB)gsinα |
 如图所示在空间中,直线MN的上方上方存在方向垂直纸面向里的匀强磁场,正方形线圈abcd的a边正好与MN 重合,线圈绕a点逆时针匀速旋转,在一个周期T内,线圈中产生的感应电流i随时间t变化的i-t图象正确的是( )
如图所示在空间中,直线MN的上方上方存在方向垂直纸面向里的匀强磁场,正方形线圈abcd的a边正好与MN 重合,线圈绕a点逆时针匀速旋转,在一个周期T内,线圈中产生的感应电流i随时间t变化的i-t图象正确的是( )



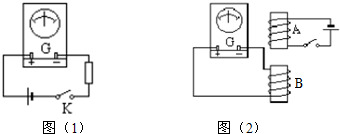
 现代技术中,传感器是指这样一类元件:它能够将诸如力、温度、光、声、化学成分等大量电学量按照一定规律转换为电学量.如图所示的装置就是一种测压强的传感器.图中A、B为大小、形状完全相同的金属板,它们构成一个电容器,其中A板被固定,两金属板的正对面积为S.金属板间空气的介电常数为ε,静电力常量为k.C、D是两根完全一样的轻质弹簧,它们的劲度系数为k0.两弹簧一端固定,另一端与金属板B上的绝缘杆相连.传感器未工作时,弹簧处于自然长度,两金属板间的距离为d0.
现代技术中,传感器是指这样一类元件:它能够将诸如力、温度、光、声、化学成分等大量电学量按照一定规律转换为电学量.如图所示的装置就是一种测压强的传感器.图中A、B为大小、形状完全相同的金属板,它们构成一个电容器,其中A板被固定,两金属板的正对面积为S.金属板间空气的介电常数为ε,静电力常量为k.C、D是两根完全一样的轻质弹簧,它们的劲度系数为k0.两弹簧一端固定,另一端与金属板B上的绝缘杆相连.传感器未工作时,弹簧处于自然长度,两金属板间的距离为d0.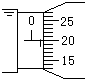 有一电阻丝阻值在100Ω-200Ω之间,额定功率为0.25W,现用伏安法准确测量它的阻值,实验室除有导线和电键外还备有
有一电阻丝阻值在100Ω-200Ω之间,额定功率为0.25W,现用伏安法准确测量它的阻值,实验室除有导线和电键外还备有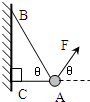 如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.
如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.