题目内容
6.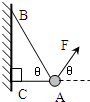 如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.
如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.
分析 对A球受力分析,受到拉力F,重力mg,两根细绳的拉力FB、FC,根据共点力平衡条件列方程,然后根据两根细线的拉力都要大于或等于零分析判断.
解答 解:物体A受重力、拉力F、AC绳拉力、AB绳的拉力,作出A受力图,如图所示:
由平衡条件有:
Fcosθ-F2-F1cosθ=0,
Fsinθ+F1sinθ-mg=0
要使两绳都能绷直,则有:
F1≥0
F2≥0
由以上各式可解得F的取值范围为:
$\frac{20}{3}$$\sqrt{3}$N≤F≤$\frac{40}{3}$$\sqrt{3}$N
答:拉力F的大小范围为$\frac{20}{3}$$\sqrt{3}$N≤F≤$\frac{40}{3}$$\sqrt{3}$N.
点评 本题关键是对小球受力分析,列平衡方程,然后找出最大和最小两种临界情况讨论即可.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
17. 物体P、Q叠放在一起,如图所示.现从某一高度由静止释放,若不计空气阻力,则它们在下落过程中( )
物体P、Q叠放在一起,如图所示.现从某一高度由静止释放,若不计空气阻力,则它们在下落过程中( )
 物体P、Q叠放在一起,如图所示.现从某一高度由静止释放,若不计空气阻力,则它们在下落过程中( )
物体P、Q叠放在一起,如图所示.现从某一高度由静止释放,若不计空气阻力,则它们在下落过程中( )| A. | P对Q有向下的弹力 | B. | P、Q间无相互作用的弹力 | ||
| C. | Q对P的弹力小于P的重力 | D. | P对Q的弹力小于Q的重力 |
1. 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )| A. | 变小 | B. | 变大 | C. | 不变 | D. | 无法确定 |
11. 在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )
在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )
 在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )
在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )| A. | P点的运动轨迹是抛物线的一部分 | B. | P点的运动轨迹是圆弧的一部分 | ||
| C. | P点的速度大小为$\frac{v_0}{2sinθ}$ | D. | P点的速度大小为v0cosθ |
16.关于路程和位移,下列说法正确的是( )
| A. | 物体通过的路程不同,但位移可能相同 | |
| B. | 物体沿某一直线运动,所通过的路程就是位移 | |
| C. | 物体的位移为零,则物体一定没运动 | |
| D. | 物体通过一段路程以后,位移必定发生变化 |
 如图所示在水平地面O处固定一竖直挡板OM段光滑,M点右侧粗糙,质量为m,带电量为+q的粗糙物块a恰能静止于M点,有一质量为2m,带电量也为+q的光滑物块b以初速度v0=$\sqrt{\frac{gL}{2}}$从N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连.每次ab与档板碰撞后均原速率弹回,整个装置牌水平向左的匀强电场中,且电场强度E=$\frac{mg}{2q}$.物块a,b均视为质点,且滑块受的最大静摩擦力等于滑动摩擦力,求:
如图所示在水平地面O处固定一竖直挡板OM段光滑,M点右侧粗糙,质量为m,带电量为+q的粗糙物块a恰能静止于M点,有一质量为2m,带电量也为+q的光滑物块b以初速度v0=$\sqrt{\frac{gL}{2}}$从N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连.每次ab与档板碰撞后均原速率弹回,整个装置牌水平向左的匀强电场中,且电场强度E=$\frac{mg}{2q}$.物块a,b均视为质点,且滑块受的最大静摩擦力等于滑动摩擦力,求: 提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(-L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场.已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用.
提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(-L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场.已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用.
 有一种“傻瓜”照相机,其光圆(进光孔径)随被拍摄物体的高度自动调节,而快门(曝光时间)是固定不变的,实验者从某砖墙的高处使一个石子自由落下,拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹,已知该照相机的曝光时间为0.02s,每块砖的平均厚度为6cm,试估算拍摄到的石子从距位置A多高处开始下落的?
有一种“傻瓜”照相机,其光圆(进光孔径)随被拍摄物体的高度自动调节,而快门(曝光时间)是固定不变的,实验者从某砖墙的高处使一个石子自由落下,拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹,已知该照相机的曝光时间为0.02s,每块砖的平均厚度为6cm,试估算拍摄到的石子从距位置A多高处开始下落的?