题目内容
如图所示，在虚线MN的上方存在磁感应强度为B的匀强磁场，方向垂直纸面向里．质子和α粒子以相同的速度v0由MN上的O点进人磁场区域，v0与MN和磁场方向均垂直．最后它们分别从MN上的P、Q两点离开磁场．已知质子的质量为m，电荷量为e，α粒子的质量为4m，电荷量为2e，不计两粒子的重力和它们之间的相互作用力，求：
（1）P、Q两点间的距离；
（2）α粒子在磁场中的运动时间．
（1）P、Q两点间的距离；
（2）α粒子在磁场中的运动时间．
（1）质子进入磁场后做半径为R1的匀速圆周运动，洛伦兹力提供向心力：ev0B=m
；
解得：R1=
质子离开磁场时距O的距离：d1=2R1=
同理，α粒子在磁场中的运动半径：R2=
=
α粒子离开磁场时距O的距离：d2=2R2=
由此可以看出质子由P点离开磁场，α粒子由Q点离开磁场P、Q两点间的距离：d=d2-d1=
（2）α粒子在磁场中的运动的周期为T，则：T=
=
=
粒子运动的时间：t=
=
答：（1）P、Q两点间的距离
；
（2）α粒子在磁场中的运动时间
| ||
| R1 |
解得：R1=
| mv0 |
| eB |
质子离开磁场时距O的距离：d1=2R1=
| 2mv0 |
| eB |
同理，α粒子在磁场中的运动半径：R2=
| 4mv0 |
| 2eB |
| 2mv0 |
| eB |
α粒子离开磁场时距O的距离：d2=2R2=
| 4mv0 |
| eB |
由此可以看出质子由P点离开磁场，α粒子由Q点离开磁场P、Q两点间的距离：d=d2-d1=
| 2mv0 |
| eB |
（2）α粒子在磁场中的运动的周期为T，则：T=
| 2πR |
| v |
| 2π?4m |
| 2e?B |
| 4πm |
| eB |
粒子运动的时间：t=
| T |
| 2 |
| 2πm |
| eB |
答：（1）P、Q两点间的距离
| 2mv0 |
| eB |
（2）α粒子在磁场中的运动时间
| 2πm |
| eB |
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
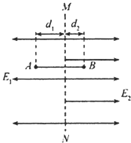（2011?福建）反射式速调管是常用的微波器件之一，它利用电子团在电场中的振荡来产生微波，其振荡原理与下述过程类似．如图所示，在虚线MN两侧分别存在着方向相反的两个匀强电场，一带电微粒从A点由静止开始，在电场力作用下沿直线在A、B两点间往返运动．已知电场强度的大小分别是E1=2.0×103N/C和E2=4.0×103N/C，方向如图所示，带电微粒质量m=1.0×10-20kg，带电量q=1.0×10-9C，A点距虚线MN的距离d1=1.0cm，不计带电微粒的重力，忽略相对论效应．求：
如图所示，在虚线MN的上方存在磁感应强度为B的匀强磁场，方向垂直纸面向里．质子和α粒子以相同的速度v0由MN上的O点进人磁场区域，v0与MN和磁场方向均垂直．最后它们分别从MN上的P、Q两点离开磁场．已知质子的质量为m，电荷量为e，α粒子的质量为4m，电荷量为2e，不计两粒子的重力和它们之间的相互作用力，求：
如图所示，在虚线MN的上方存在磁感应强度为B的匀强磁场，方向垂直纸面向内，质子和α粒子以相同的速度v0由MN上的O点以垂直MN且垂直于磁场的方向射入匀强磁场中，再分别从MN上A、B两点离开磁场．已知质子的质量为m，电荷为e，α粒子的质量为4m，电荷为2e．忽略带电粒子的重力及质子和α粒子间的相互作用．求：
如图所示，在虚线MN的上方存在方向垂直纸面向里的匀强磁场，质子和α粒子从MN上的O点以相同的速度v0（v0在纸面内且与MN的夹角为θ，θ＜90°）同时射入匀强磁场中，再分别从MN上A、B两点离开磁场，A、B距离为d．已知质子的质量为m，电荷为e．不计重力及质子和α粒子间的相互作用．求：