题目内容
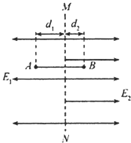 (2011?福建)反射式速调管是常用的微波器件之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似.如图所示,在虚线MN两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动.已知电场强度的大小分别是E1=2.0×103N/C和E2=4.0×103N/C,方向如图所示,带电微粒质量m=1.0×10-20kg,带电量q=1.0×10-9C,A点距虚线MN的距离d1=1.0cm,不计带电微粒的重力,忽略相对论效应.求:
(2011?福建)反射式速调管是常用的微波器件之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似.如图所示,在虚线MN两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动.已知电场强度的大小分别是E1=2.0×103N/C和E2=4.0×103N/C,方向如图所示,带电微粒质量m=1.0×10-20kg,带电量q=1.0×10-9C,A点距虚线MN的距离d1=1.0cm,不计带电微粒的重力,忽略相对论效应.求:(1)B点距虚线MN的距离d2;
(2)带电微粒从A点运动到B点所经历的时间t.
分析:对带电粒子运用动能定理研究A到B得过程,注意其中电场力做功的表达.
抓住粒子在同一电场中做的是匀变速直线运动,运用运动学公式求出时间.
抓住粒子在同一电场中做的是匀变速直线运动,运用运动学公式求出时间.
解答:解:(1)带电微粒由A运动到B的过程中,由动能定理有:
|q|E1d1-|q|E2d2=0-0=0 ①
由①式解得 d2=
=0.50cm ②
(2)设微粒在虚线MN两侧的加速度大小分别为a1、a2,由牛顿第二定律有:
|q|E1=ma1 ③
|q|E2=ma2 ④
设微粒在虚线MN两侧运动的时间分别为t1、t2,由运动学公式有:
d1=
⑤
d2=
⑥
又 t=t1+t2 ⑦
由②③④⑤⑥⑦式解得:
t=1.5×10-8s
答:(1)B点距虚线MN的距离是d2=0.50cm;
(2)带电微粒从A点运动到B点所经历的时间是1.5×10-8s.
|q|E1d1-|q|E2d2=0-0=0 ①
由①式解得 d2=
| E1d1 |
| E2 |
(2)设微粒在虚线MN两侧的加速度大小分别为a1、a2,由牛顿第二定律有:
|q|E1=ma1 ③
|q|E2=ma2 ④
设微粒在虚线MN两侧运动的时间分别为t1、t2,由运动学公式有:
d1=
| a1t12 |
| 2 |
d2=
| a2t22 |
| 2 |
又 t=t1+t2 ⑦
由②③④⑤⑥⑦式解得:
t=1.5×10-8s
答:(1)B点距虚线MN的距离是d2=0.50cm;
(2)带电微粒从A点运动到B点所经历的时间是1.5×10-8s.
点评:动能定理的应用范围很广,可以求速度、力、功、位移等物理量.
在不同的物理情境下,所受的力不同,就有不同的加速度,我们要分过程分析力与运动.
对于时间的求解我们更多的是运用牛顿第二定律结合运动学公式知识去解决.
在不同的物理情境下,所受的力不同,就有不同的加速度,我们要分过程分析力与运动.
对于时间的求解我们更多的是运用牛顿第二定律结合运动学公式知识去解决.

练习册系列答案
相关题目