一个运动员在地面跳远.最远可跳L．如果它立在船头.船头离河岸的距离为L.他想从船头跳到岸上.下列说法正确的是( )A．他不可能跳到岸上B．他有可能跳到岸上C．他先从船头到船尾.再从船尾跑到船头起跳可跳到岸上D．如果它原来站在船尾.然后从船尾跑到船头起跳可跳到岸上题目和参考答案——青夏教育精英家教网—

题目内容

16．一个运动员在地面跳远，最远可跳L．如果它立在船头，船头离河岸的距离为L，他想从船头跳到岸上，下列说法正确的是（　　）

	A．	他不可能跳到岸上
	B．	他有可能跳到岸上
	C．	他先从船头到船尾，再从船尾跑到船头起跳可跳到岸上
	D．	如果它原来站在船尾，然后从船尾跑到船头起跳可跳到岸上

分析人从船头跳出的过程，人和船组成的系统动量守恒，人与船的合动量为零．由此动量守恒定律和能量守恒定律分析即可．

解答解：根据动量守恒定律知：人从在船上起跳的过程，人与船的合动量为零，可知人起跳时船获得与人方向相反的速度，再结合能量守恒定律可知，人跳出时相对地面的速度比在地面上起跳时的速度小，所以人不可能跳到岸上；
即使他从船头跑到船尾，再返回船头助跑起跳，跑动的过程，船与人系统仍然满足合动量为零，即船也会向相反方向跑去，故人还是不能跳到岸上；故A正确，BCD错误．
故选：A

点评本题的关键要抓住：无论是哪种情况，船和船上的人都满足系统动量守恒和能量守恒，根据人相对于地面的速度来判断．

练习册系列答案

	A．	向心加速度将变小		B．	线速度将变小
	C．	周期将变大		D．	加速度将变大

7．读出下面游标卡尺和螺旋测微器的读数：

①4.60mm；
②3.140mm．

4．

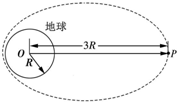2015年12月10日，我国成功将中星1C卫星发射升空，卫星顺利进入预定转移轨道．如图所示是某卫星沿椭圆轨道绕地球运动的示意图，已知地球半径为R，地球表面的重力加速度为g，卫星远地点P距地心O的距离为3R．则（　　）

	A．	卫星在远地点的速度大于$\frac{\sqrt{3gR}}{3}$
	B．	卫星经过远地点时速度最小
	C．	卫星经过远地点时的加速度大小为$\frac{g}{9}$
	D．	卫星经过远地点时加速，卫星将不能再次经过远地点

11．氢原子处于能级为-13.6eV的基态，若直接激发到第四能级上，需吸收12.75eV的能量，从该激发态跃迁，可以辐射出最长波长λ=1.88×10^-6m的电磁波．（氢原子在第n能级的能量E_n=$\frac{{E}_{1}}{{n}^{2}}$，普朗克常量h=6.63×10^-34J•s，真空中光速c=3×10⁸m/s，元电荷e=1.6×10^-19C）

1．电源的输出功率P跟外电路的电阻R有关．如图所示，是研究它们关系的实验电路．为了便于进行实验和保护蓄电池，给蓄电池串联了一个定值电阻R₀，把它们一起看作新电源（图中虚线框内部分）．新电源的内电阻就是蓄电池的内电阻和定值电阻R₀之和，用r表示，电源的电动势用E表示．
①写出新电源的输出功率P跟E、r、R的关系式：$P=\frac{{{E^2}R}}{{{{（R+r）}^2}}}$．（安培表、伏特表看作理想电表）．
②在实物图中按电路图画出连线，组成实验电路．
③表中给出了6组实验数据，根据这些数据，在方格纸中画出P-R关系图线．根据图线可知，新电源输出功率的最大值约是1.05W，当时对应的外电阻约是5Ω．

U（V）	3.5	3.0	2.5	2.0	1.5	1.0
I（A）	0.2	0.3	0.4	0.5	0.6	0.7

8．如图甲所示，一轻弹簧的两端与质量分别为m₁和m₂的两物块A、B相连接，并静止在光滑的水平面上．现使A瞬时获得水平向右的速度3m/s，以此刻为计时起点，两物块的速度随时间变化的规律如图乙所示，从图象信息可得（　　）

	A．	在t₁、t₃时刻两物块达到共同速度1m/s，且弹簧都是处于压缩状态
	B．	从t₃到t₄时刻弹簧由压缩状态恢复到原长
	C．	两物体的质量之比为m₁：m₂=1：3
	D．	在t₂时刻A与B的动能之比为E_k1：E_k2=1：8

5．在双缝干涉实验中，以白光为光源，在屏幕上观察到了彩色干涉条纹．若在双缝的一缝前放一红色滤光片（只能透过红光），另一缝前放一绿色滤光片（只能透过绿光），这时（　　）

	A．	只有红色和绿色的双缝干涉，其他颜色的双缝干涉纹消失
	B．	任何颜色的双缝干涉条纹都不存在，但屏上仍有光亮
	C．	红色和绿色的双缝干涉条纹消失，其他颜色的双缝干涉条纹依然存在
	D．	屏上无任何光亮

19．做匀速圆周运动的物体，圆半径为R，转动频率为f，转速为n，以下说法正确的是（　　）

试题分类