��Ŀ����
9����ͼ1��ʾ��������ˮƽ��ɦ�=30��ǵ��㹻���⻬��������ƽ�з��ã�������ΪL=1m������˽�����ֵΪ0.5���ĵ���R������ĵ�����Բ��ƣ�����װ�ô�����ǿ�ų��У��ų�����ֱ�ڵ���ƽ��б���ϣ��Ÿ�Ӧǿ��B=1T������һ����Ϊm=0.2kg������Ϊ0.5���Ľ�������ϸ��ͨ���⻬����������ΪM=0.5kg������������ϸ���뵼��ƽ��ƽ�У�����������M�ɾ�ֹ�ͷţ����ص����˶���2m��ʼ�������˶����˶������У����뵼��ʼ�ձ��ִ�ֱ�Ӵ�����ȡ�������ٶ�g=10m/s2����
��1�������������˶�ʱ���ٶȣ�
��2�������ͷŵ���ʼ�����˶��Ĺ����У�����R�ϲ����Ľ����ȣ�
��3��������ijһ��С�ĴŸ�Ӧǿ��B1���䣬ȡ��ͬ����M����������������������������Ӧ���������˶���vֵ���õ�ʵ��ͼ����ͼ2��ʾ�������ͼ�е����ݼ������ʱ��B1��
��4���ı�Ÿ�Ӧǿ�ȵĴ�СΪB2��B2=2B1�������������䣬��������ͼ�ϻ�����Ӧ��v-Mͼ�ߣ�����˵��ͼ����M��Ľ�����������壮
���� ��1�������������˶�ʱ������ƽ�⣬���ӵ�������С����Mg����ƽ�������Ͱ�������ʽFA=$\frac{{B}^{2}{L}^{2}v}{R}$����ٶȣ�
��2���������ϻ��Ĺ����У�M���������ܼ�Сת��Ϊm���������ܡ�M��m�Ķ��ܼ���·�е����ܣ����������غ㶨��������R�ϲ����Ľ����ȣ�
��3���ɣ�1�����ٶ��������Ĺ�ϵʽ������ͼ���б����ؾ�����壬���B1��
��4�����ݺ�����ϵʽ����ͼ��
��� �⣺��1���������������˶�������ƽ��״̬��
��ƽ�������ã�Mg=mgsin��+$\frac{{B}^{2}{L}^{2}v}{R}$��
��ã�v=4 m/s��
��2����ϵͳ���������غ㶨�ɵã�
Mgs=mgssin��+2Q+$\frac{1}{2}$��M+m��v2��
��ã�Q=1.2J��
��3���Խ����ˣ���ƽ�������ã�Mg=mgsin��+$\frac{{B}^{2}{L}^{2}v}{R}$��
��v=$\frac{��Mg-mgsin�ȣ�R}{{B}^{2}{L}^{2}}$=$\frac{gR}{{B}^{2}{L}^{2}}$ M-$\frac{mgRsin��}{{B}^{2}{L}^{2}}$�٣�
��ͼ���֪��$\frac{gR}{{B}^{2}{L}^{2}}$=$\frac{10}{0.3}$����ã�B1=0.54T��
��4����v=$\frac{gR}{{B}^{2}{L}^{2}}$ M-$\frac{mgRsin��}{{B}^{2}{L}^{2}}$��֪����B2=2B1ʱ��
ͼ�ߵ�б�ʼ�СΪԭ����$\frac{1}{4}$����M��Ľ��㲻�䣬
��M��Ľ���ΪM=msin�ȣ�ͼ����ͼ��ʾ��
�𣺣�1�������������˶�ʱ���ٶ�Ϊ4m/s��
��2�������ͷŵ���ʼ�����˶��Ĺ����У�����R�ϲ����Ľ�������1.2J��
��3������ͼ�е����ݼ������ʱ��B1Ϊ0.54T��
��4��ͼ������ͼ��ʾ��
���� �����и����������ɵõ�����ʽ���ٷ���ͼ�����ѧ���壬������ѧ�����ν�ϵķ�����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�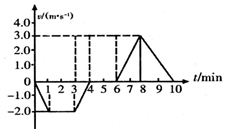 �ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������
�ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������| A�� | ����ʵ����DZ������Ϊ6m | |
| B�� | ȫ�����������ٶȵĴ�С��2m/s2 | |
| C�� | �ӿ�ʼ������ͨ������·��Ϊ720m | |
| D�� | ��DZ�����뷵�ع��̵�ƽ���ٶ���ͬ |
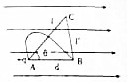 ��ͼ��ʾ���糡ǿ��ΪE����ǿ�糡�У��������Ϊ+q�ĵ����ֱ��AB������ACB������AB�˶������ھ��������Ĺ��ʹ�С��ϵ������˵����ȷ���ǣ�������
��ͼ��ʾ���糡ǿ��ΪE����ǿ�糡�У��������Ϊ+q�ĵ����ֱ��AB������ACB������AB�˶������ھ��������Ĺ��ʹ�С��ϵ������˵����ȷ���ǣ�������| A�� | ������ACB�˶�ʱ������� | B�� | ��ֱ��AB�˶�ʱ�������� | ||
| C�� | ��ֱ��AB�˶�ʱ������������ΪqEd | D�� | ��ֱ��AB�˶�ʱ������� |
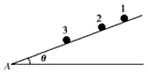 ��ͼ��ʾ���ڹ⻬��б���Ϸ���3����ͬ��С����Ϊ�ʵ㣩��С��1��2��3��б���A��ľ���ֱ�Ϊx1��x2��x3���ֽ����Ƿֱ�Ӿ�ֹ�ͷţ�����A���ʱ��ֱ�Ϊt1��t2��t3��б������Ϊ�ȣ�������˵����ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��б���Ϸ���3����ͬ��С����Ϊ�ʵ㣩��С��1��2��3��б���A��ľ���ֱ�Ϊx1��x2��x3���ֽ����Ƿֱ�Ӿ�ֹ�ͷţ�����A���ʱ��ֱ�Ϊt1��t2��t3��б������Ϊ�ȣ�������˵����ȷ���ǣ�������| A�� | $\frac{{x}_{1}}{{t}_{1}}$$��\frac{{x}_{2}}{{t}_{2}}$$��\frac{{x}_{3}}{{t}_{3}}$ | B�� | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C�� | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{2}}$=$\frac{{x}_{3}}{{{t}_{3}}^{2}}$ | D�� | ����������$\frac{x}{{t}_{2}}$��ֵ��С |
 ����ͼ��ʾ�Ĵֲ�ˮƽ���Ϲ̶�һ��Ǧ�=37���������б��������ˮƽ����б����B��ƽ�����ӣ��ֽ�һ����Ϊm=2kg��С���徲����ˮƽ���A�㣬��ijʱ�����С����ʩ��һˮƽ���ҵ�������F����������F��С�����λ�Ƶı仯������ͼ��С�����ܾ�B������б��������С�����ڹ�B��ʱ�Ļ�е����ʧ���Բ��ƣ���֪С������ˮƽ���Լ���б����Ķ�Ħ��������Ϊ��=0.5��AB�����ľ���Ϊx=4m��g=10m/s2��sin37��=0.6��cos37��=0.8����
����ͼ��ʾ�Ĵֲ�ˮƽ���Ϲ̶�һ��Ǧ�=37���������б��������ˮƽ����б����B��ƽ�����ӣ��ֽ�һ����Ϊm=2kg��С���徲����ˮƽ���A�㣬��ijʱ�����С����ʩ��һˮƽ���ҵ�������F����������F��С�����λ�Ƶı仯������ͼ��С�����ܾ�B������б��������С�����ڹ�B��ʱ�Ļ�е����ʧ���Բ��ƣ���֪С������ˮƽ���Լ���б����Ķ�Ħ��������Ϊ��=0.5��AB�����ľ���Ϊx=4m��g=10m/s2��sin37��=0.6��cos37��=0.8���� ��ͼ��ʾ��һ��ˮƽ��н�Ϊ��=37�����б����ƽ�е������㹻����һ���֣�ab��cd����֮�䣩���ڴ�ֱ����ƽ�����ϵ���ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȴ�СΪB=2T���������L=1m���ײ�����һ��ֵΪR1=2���Ķ�ֵ���裬�ڴų��߽�cd�ڲ����������Ե������סһ����ΪM=2kg������䲿�ֵ���ΪR2=3���ĵ����MN����ʹһ����Ϊm=0.5kg������䲿�ֵ���Ϊr=0.3���ĵ����PQ�Ӵų��ϱ߽�ab�Ϸ��������ij�������»�������ų�ʱ���ٶ�v0=3m/s���������ʼ���뵼��Ӵ����ã��Ҵ�ֱ������ã�������費�ƣ�����һ��Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8��
��ͼ��ʾ��һ��ˮƽ��н�Ϊ��=37�����б����ƽ�е������㹻����һ���֣�ab��cd����֮�䣩���ڴ�ֱ����ƽ�����ϵ���ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȴ�СΪB=2T���������L=1m���ײ�����һ��ֵΪR1=2���Ķ�ֵ���裬�ڴų��߽�cd�ڲ����������Ե������סһ����ΪM=2kg������䲿�ֵ���ΪR2=3���ĵ����MN����ʹһ����Ϊm=0.5kg������䲿�ֵ���Ϊr=0.3���ĵ����PQ�Ӵų��ϱ߽�ab�Ϸ��������ij�������»�������ų�ʱ���ٶ�v0=3m/s���������ʼ���뵼��Ӵ����ã��Ҵ�ֱ������ã�������費�ƣ�����һ��Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8�� �ó�Ϊl��ϸ������һ����Ϊm���������Ϊ+Q��С��������ˮƽ���������Ҵ�СΪE����ǿ�糡�У���ͼ��ʾ���ֽ�С��̶�����������·���$\overline{OA}$=1��λ��A����Ȼ���ͷ�С����֪�糡�������������������ܵ������������
�ó�Ϊl��ϸ������һ����Ϊm���������Ϊ+Q��С��������ˮƽ���������Ҵ�СΪE����ǿ�糡�У���ͼ��ʾ���ֽ�С��̶�����������·���$\overline{OA}$=1��λ��A����Ȼ���ͷ�С����֪�糡�������������������ܵ������������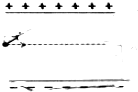 ��ͼ��ʾ��ƽ�а�������ϼ�������磬������Ϊd��һ����Ϊm�����Ϊq����������뼫���60��ǵķ���СΪv0���ٶ��ɼ��������λ������糡�����Ӹպ���ƽ�м�����ٶ��ؼ����Ե�����������ij���L��
��ͼ��ʾ��ƽ�а�������ϼ�������磬������Ϊd��һ����Ϊm�����Ϊq����������뼫���60��ǵķ���СΪv0���ٶ��ɼ��������λ������糡�����Ӹպ���ƽ�м�����ٶ��ؼ����Ե�����������ij���L��